пњљпњљ6пњљпњљпњљ№§ќЉпњљпњљпњљ :
![]()
пњљпњљпњљпњљт∞Ј§пњљпњљЁ§пњљ пњљƒ°пњљпњљќЄпњљпњљпњљпњљпњљ–§пњљпњљпњљ пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ«Њпњљпњљпњљпњљпњљпњљл°£
㧮–°пњљ
![]() ,
,
![]() пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
![]() пњљтЉ®§пњљпњљЋ§ѕ°пњљ
пњљтЉ®§пњљпњљЋ§ѕ°пњљ
∆±пњљЌ§Ћ°пњљ
![]()
![]()
![]() ,
,
![]()
![]()
![]() пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљпњљпњљ–§пњљпњљ∆°пњљ
![]() пњљтЉ®§пњљпњљЋ§ѕ°пњљ
пњљтЉ®§пњљпњљЋ§ѕ°пњљ
пњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљпњљ
пњљпњљпњљпњљпњљпњљќ©пњљƒ§пњљпњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљтЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљ
пњљтЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
&dotfill#dotfill;
![]()
![]()
![]() пњљЋ§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ•ќ•пњљпњљпњљ
пњљЋ§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ•ќ•пњљпњљпњљ
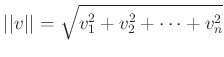
пњљпњљпњљпњљпњљпњљпњљпњљл°£пњљпњљпњљќ§»§пњљпњљпњљ
пњљпњљпњљ §к§њпњљƒ°пњљ(пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ)
пњљпњљпњљћ§Ћ°пњљ
![]()
![]()
![]() пњљпњљ
пњљпњљ ![]() пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљ»§пњљпњљпњљпњљпњљ
![]()
![]() пњљпњљпњљпњљ ђпњљпњљпњљпњљ
пњљпњљпњљпњљ ђпњљпњљпњљпњљ ![]() пњљпњљ
пњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљ»§пњљпњљпњљ(пњљћЊпњљпњљпњљпњљЋіЎ§пњљпњљпњљ)пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљпњљ»Є∆§–§пњљл°£ пњљпњљпњљпњљпњљпњљ»§ѕ°пњљпњљ÷ґпњљпњљпњљпњљпњљё§ё§ §пњљпњљпњљпњљпњљ„§»§пњљпњљпњљпњљпњљпњљ»§ќњпњљпњљпњљ≈™пњљпњљ…љпњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљ»§пњљпњљпњљпњљпњљќ§пњљў°пњљпњљпњљпњљЋ§пњљпњљ∆°пњљпњљ÷±у§§°„°÷ґб§§пњљ„°÷§ƒ§ §пњљпњљ√§∆§пњљпњљпњљ„§ §…§пњљ пњљпњљ«∞пњљпњљпњљпњљпњљ≈™пњљЋЉпњљк∞Јпњљпњљпњљпњљи§¶пњљЋ§пњљпњљпњљпњљпњљќ§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£ пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљѕЄпњљпњљпњљпњљпњљЎ§Ћ§пњљпњљпњљпњљпњљпњљпњљпњљ—љпњљпњљ„§ ∞пњљпњљ÷§пњљпњљпњљпњљ∆§пњљпњљ∆°пњљ пњљ §пњљ«њпњљпњљЎ§пњљЎ§”§пњљпњљпњљпњљЌ§ѕ°пњљпњљг§®пњљпњљпњљпњљ ђпњљпњљ ђпњљЎ§ќ≥Ўљпњљпњљпњљпњљ¬є‘§пњљпњљ∆≥Ўљпњљпњљпњљпњљ∆§я§пњљќ§пњљ пњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљ÷ґпњљпњљпњљпњљ„§»§пњљпњљпњљпњљпњљпњљ’Љпњљпњљќ§пњљпњљпњљпњљ≈™пњљпњљ…љпњљпњљпњљ«§пњљпњљл§ђпњљпњљ пњљпњљпњљпњљпњљ«§ѕ§пњљпњљпњљпњљё§«§пњљ∆Іпњљяєпњљпњљё§ §пњљпњљпњљпњљ»§Ћ§пњљпњљл°£
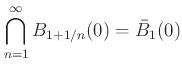
пњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљћ§Ћ°пњљпњљпњљпњљпњљпњљпњљќ£пњљпњљƒ§ќґпњљпњљпњљпњљпњљ ђпњљѕ≥пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ ћµпњљ¬Єƒ§ќґпњљпњљпњљпњљпњљ ђпњљѕ≥пњљпњљпњљпњљпњљ»§ѕЄ¬§пњљ §пњљпњљпњљ