��4���ܤμ��� :
![]()
�ޤ�������������
�������������ޤ�
����δط��������ǽҤ٤뤳�Ȥ�褯���롣
����������������?
����������Ȥ�ʢ�δط��ˤ���ΤǤ��ä��������� ![]() ��
�� ![]() ���б����뽸����Ū�ʳ�ǰ��¸�ߤ��롣
���б����뽸����Ū�ʳ�ǰ��¸�ߤ��롣
Ʊ�ͤˡ����� ![]() �ΰ�İ�Ĥθ�
�ΰ�İ�Ĥθ� ![]() ���Ф��ƽ���
���Ф��ƽ��� ![]() ��Ϳ����줿�Ȥ��������²
��Ϳ����줿�Ȥ��������²
![]() ��Ϳ��
��줿�Ȥ�����
��Ϳ��
��줿�Ȥ�����![]() �Τ��Ȥ�²��ź�������ȸƤ֡�
�Τ��Ȥ�²��ź�������ȸƤ֡�
���������Ͻ���²�����̤ʾ��Ǥ��롣
![]() �Τ��Ȥ�
�Τ��Ȥ�
![]() �Τ褦�˽Ƥ���ΤǤ��롣
�Τ褦�˽Ƥ���ΤǤ��롣
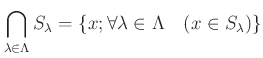
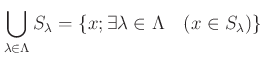
�ˤ��������롣
������ˤĤ��Ƥϡ����ζ�����ʬ
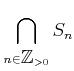
�Τ��Ȥ�
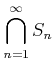
�Τ��Ȥ����Ȥ�¿�����½����Ʊ�͡�
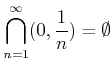
�Ǥ��뤳�Ȥ��ʤ����� ���դε�����������Ȥ��äơ�����ҤȤĤ�����ʤ�����Τ��Ȥ� ����Ǥ��롣
![$\displaystyle \bigcap_{\epsilon>0} (-\infty, 1+\epsilon) =(-\infty, 1]
$](img25.png)
�Ǥ��뤳�Ȥ��ʤ����� ���դϷ��줷����
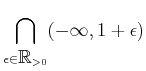 �Ȥʤ�Ȥ����Ǥ��뤬����Τ褦�˾�ά���뤳�Ȥ������ˤ��Ƥ��롣
�Ȥʤ�Ȥ����Ǥ��뤬����Τ褦�˾�ά���뤳�Ȥ������ˤ��Ƥ��롣
�����Ƚ����ʢ�δط��ޤ����Ѥ��ơ�����Ū�ʻ����� ���绻��ɽ�����Ƥ��ޤ��ޤ����Ω�Ľ�����뤳�Ȥ��Ǥ��롣 �����������¬�����κǽ�ΤȤ����ʤɤϤȤ��ˤ��μ�ˡ�������˸���롣
��Ȥ��ơ� ���Τ褦�ʤ��Ȥ�ͤ��褦��
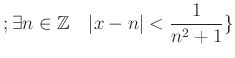 |
||
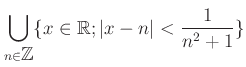 |
||
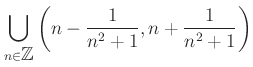 |
���ν���ϡ�Ĺ�������� ![]() ��ͭ�� (
��ͭ�� (
![]() )
�Ǥ���褦�ʳ���֤��½���Ǥ��ꡢ
)
�Ǥ���褦�ʳ���֤��½���Ǥ��ꡢ
![]() ����ʬ����Ȥ��ƴޤ�Ǥ��롣
����ʬ����Ȥ��ƴޤ�Ǥ��롣
Ʊ�ͤˤ��ơ�Ǥ�դ�
![]() ���Ф��ơ�
���Ф��ơ�
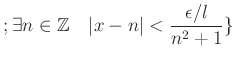 |
||
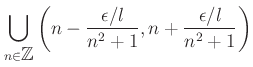 |
![% latex2html id marker 1267
$\displaystyle \{ x \in [0,1] ; \forall n \in {\mbo...
... \in {\mbox{${\mathbb{Z}}$}} \quad (\vert\frac{m}{n} -x\vert<\frac{1}{n^3})) \}$](img41.png) |
||
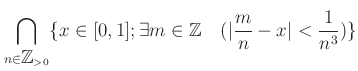 |
||
![$\displaystyle \bigcap_{n \in {\mbox{${\mathbb{Z}}$}}_{>0}} \bigcup_{m \in {\mbox{${\mathbb{Z}}$}}} \{ x \in [0,1] : \vert\frac{m}{n} -x\vert<\frac{1}{n^3} \}$](img43.png) |
||
![$\displaystyle \bigcap_{n \in {\mbox{${\mathbb{Z}}$}}_{>0}} \bigcup_{m \in {\mbo...
...[0,1] \cap \big( \frac{m}{n} -\frac{1}{n^3}, \frac{m}{n} +\frac{1}{n^3} \big) )$](img44.png) |
||
![$\displaystyle [0,1]\cap (\bigcap_{n \in {\mbox{${\mathbb{Z}}$}}_{>0}} \bigcup_{...
...bb{Z}}$}}} \big( \frac{m}{n} -\frac{1}{n^3}, \frac{m}{n} +\frac{1}{n^3} \big) )$](img45.png) |
���Τ��Ȥϡ��¤ϡ�
![]()
![]() ��Ĺ�������¤�ͭ�¤γ���֤��½����
ʤ���뤳�Ȥ�ɽ���Ƥ��롣
��Ĺ�������¤�ͭ�¤γ���֤��½����
ʤ���뤳�Ȥ�ɽ���Ƥ��롣