


Next: About this document ...
代数学II要約 No.7
第7回目の主題 :

定義 7.1
環
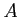
上の加群
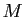
の元
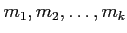
に対して、
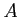
-準同型
の核
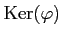
の元のことを
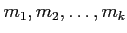
の
関係式と呼び、
その全体のなす加群
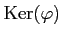
のことを
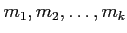
の
関係式のなす加群と呼ぶ。
以下では、次のような変換を考える。
- 変換1.
-
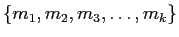 の順序を入れ換える。
の順序を入れ換える。
- 変換2.
-
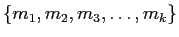 の代わりに
それを
の代わりに
それを
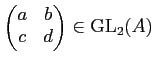 で「ひねった」
で「ひねった」
を考える。
- 変換3.
-
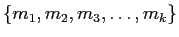 の代わりに
の代わりに 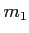 を
を
に置き換えたもの
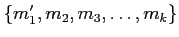 を考える。
を考える。
(変換3)は(変換1), (変換2)を有限回組み合わせて得られることが
わかるので
以下の議論で必須ではない。
定義 7.2 (この講義だけで通じる記号)
可換 PID
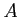
と、その上の加群
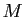
が与えられていて、
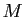
は
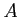
上
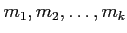
で生成されているとする。
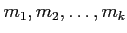
を(変換1), (変換2), (変換3) を
有限回繰り返して得られる
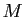
の元の組

の全体を
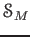
と書くことにする。
補題 7.3 (変換1)
,(変換2),(変換3)の形の変換は(同じ形の)逆変換をもつ。
とくに、
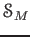
の各元
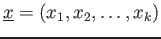
にたいして、
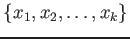
も
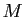
を生成する。
補題 7.4
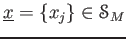
が、関係式
を満たしたとする。
とおいて、
と書こう。このとき、
を最初の元として持つような
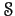
の元

が存在する。
この
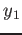
は
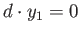
を満たすことにも注意しよう。
定理 7.6
可換 PID
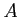
上の有限生成加群
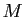
が与えられているとする。
このとき、
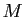
の生成系
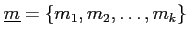
にたいして、
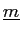
を(変換1),(変換2),(変換3)を有限回繰り返すことにより、
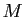
の新しい生成系
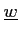
であって、
(巡回加群の直和)となるものが存在する。
一つの元で生成される加群を巡回加群と呼ぶのでした。
命題 7.8 (定理の言い換え)
可換 PID
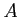
上の任意の有限生成加群
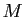
は巡回
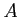
加群の直和に同型である。
ゆえに、ある
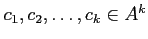
と
なる同型が存在する。
(ただの)加群は
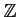 -加群のことと同じであって、
-加群のことと同じであって、
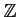 は
は 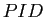 であることから、
つぎの(大変有用かつ重要な)系が成り立つ。
であることから、
つぎの(大変有用かつ重要な)系が成り立つ。
系 7.9 (有限生成アーベル群の基本定理)
任意の有限生成アーベル群は巡回群の有限個の直和である。
命題 7.10
可換 PID
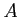
のイデアルの増加列
は必ず有限で止まる。すなわち、ある
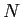
があって、
が成り立つ。



Next: About this document ...
2013-06-05
![]()
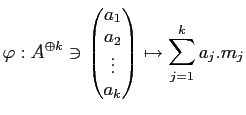
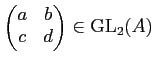 で「ひねった」
で「ひねった」
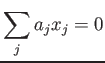
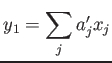
![]() -加群のことと同じであって、
-加群のことと同じであって、
![]() は
は ![]() であることから、
つぎの(大変有用かつ重要な)系が成り立つ。
であることから、
つぎの(大変有用かつ重要な)系が成り立つ。