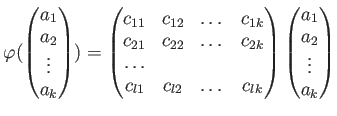Next: About this document ...
代数学II要約 No.5
第5回目の主題 :

◎有限生成加群 (再掲)
定義 5.1
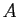
-加群
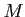
が有限個の元で生成されるとき、
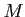
を
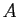
上の
有限生成加群と呼ぶ。
例 5.2
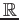
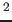
は 有限生成
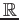
-加群だが、
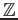
-加群としては有限生成ではない。
補題 5.3
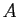
-加群
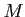
が有限個の元

で生成されるとき、
- 写像
は 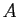 -加群の全射準同型である。
-加群の全射準同型である。
-
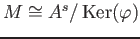 .
.
**
一般に、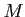 の
の 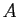 -加群としての生成元
-加群としての生成元
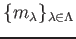 を
とれば、全射
を
とれば、全射 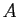 -準同型
-準同型
が定義されて、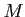 は自由加群の剰余加群として表現されることが分かる。
**
は自由加群の剰余加群として表現されることが分かる。
**
自由加群から一般の加群への準同型は次のように「生成元の行き先」で定まる。
うえのことは、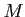 が適当な有限性の条件を満足すれば(つまり、有限表示を持てば)、
が適当な有限性の条件を満足すれば(つまり、有限表示を持てば)、
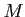 は
上のような準同型の余核として得られることを示している。
は
上のような準同型の余核として得られることを示している。
命題 5.6
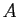
は可換環であるとする。このとき、
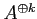
から
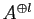
への任意の
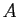
-準同型
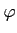
は、
と書ける。
例 5.7
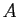
-加群
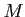
が 一つの元で生成されている場合、
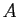
の左イデアル
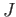
があって、
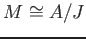
となる。
さらに、
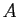
が可換で、かつ PID であれば、
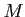
は
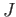
はやはり
一つの元で生成されて、
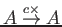
の余核
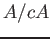
と同型になる。



Next: About this document ...
2013-05-16
![]()
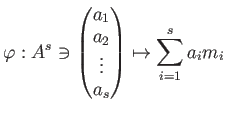
![]() の
の ![]() -加群としての生成元
-加群としての生成元
![]() を
とれば、全射
を
とれば、全射 ![]() -準同型
-準同型

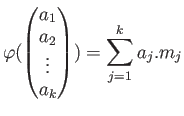
![]() が適当な有限性の条件を満足すれば(つまり、有限表示を持てば)、
が適当な有限性の条件を満足すれば(つまり、有限表示を持てば)、
![]() は
上のような準同型の余核として得られることを示している。
は
上のような準同型の余核として得られることを示している。