![]()
抽象的ベクトル空間、ベクトル空間の部分空間。一次独立性
実数直線も、
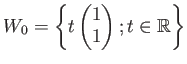
も、「同じ形」をしている。 このような2つを同時に扱うのには、成分を見るのではなく、 和と、スカラー倍という道具のみを用いて記述することが 大事になる。 そもそも、成分を扱ってばかりいるのではベクトルを研究する意味がない。
上で「
![]() 」とあるところをことごとく「
」とあるところをことごとく「
![]() 」で置き換えると、
複素数体上のベクトル空間の定義になる。更に、
」で置き換えると、
複素数体上のベクトル空間の定義になる。更に、
![]() のところを
体(加減乗除について閉じたような集合)
のところを
体(加減乗除について閉じたような集合)![]() で置き換えて、
で置き換えて、![]() 上のベクトル空間
の定義を与えることができる。
上のベクトル空間
の定義を与えることができる。
を満たすときにいう。
要するに、一次従属であるとは、与えられたベクトルの間に 関係式が存在することである。 一次独立かそうでない(一次従属)か、 は和とスカラー倍のみを用いて記述されており、 成分の値については直接は言及していない。いかにも線形代数的な概念である。
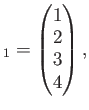
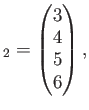
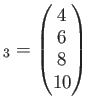
で定めると、
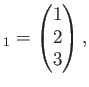
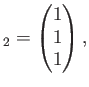
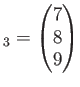
で定めると、
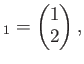
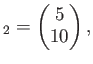
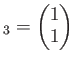
で定めると、
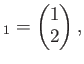
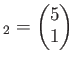
とおくと、
とすると、
で、これを解くと
※レポート問題
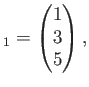
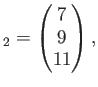
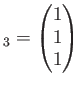
とおくと、