


Next: About this document ...
пњљпњљпњљпњљпњљ»љпњљпњљпњљпњљпњљпњљпњљ No.14
пњљпњљ14пњљпњљпњљ№§ќЉпњљпњљпњљ :

пњљпњљпњљ 14.1 (пњљпњљ)
пњљпњљпњљпњљ
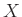
пњљпњљпњљпњљ ђпњљпњљпњљпњљпњљ¬≤
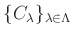
пњљпњљ
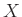
пњљпњљ
пњљпњљпњљй•є ђпњљпњљ (
ђпњљпњљпњљ»§пњљпњљпњљпњљ)пњљ«§пњљпњљпњљ»§ѕ°пњљпњљƒ§пњљпњљќ§пњљпњљ»§пњљпњљпњљпњљпњљќ©пњљƒ§»§пњљпњљЋЄпњљпњљпњљпњљпњљ
-
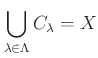 .
.
-
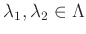 ,
,
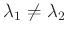 пњљ §пњљпњљ
пњљ §пњљпњљ
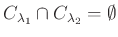 .
.
ћњпњљпњљ 14.3
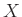
пњљпњљ∆±пњљЌіЎЈпњљ
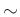
пњљпњљпњљпњљё§√§∆§пњљпњљпњљ»§пњљпњљл°£пњљпњљпњљќ§»§пњљпњљпњљ
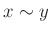
пњљпњљпњљЁ§пњљпњљЋ§пњљ√§∆°пњљ
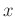
пњљпњљ
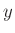
пњљпњљ∆±пњљпњљпњљпњљпњљй•єпњљпњљпњљЁ§пњљпњљпњљ
пњљпњљпњљл§≥пњљ»§пњљ
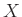
пњљќ•пњљпњљй•є ђпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљЋ§ §л°Ґпњљ §пњљ §пњљ



Next: About this document ...
2012-07-19
![]()
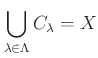 .
.