


Next: Bibliography
Commutative algebra
Yoshifumi Tsuchimoto

DEFINITION 01.1
A (unital associative)
ring is a set
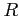
equipped with two binary operations
(addition (``+'') and multiplication (``
'')) such that
the following axioms are satisfied.
- Ring-1.
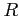 is an additive group with respect to the addition.
is an additive group with respect to the addition.
- Ring-2.
- distributive law holds. Namely, we have
- Ring-3.
- The multiplcation is associative.
- Ring-4.
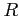 has a multiplicative unit.
has a multiplicative unit.
In this lectuer we are mainly interested in commutative rings,
that means, rings on which the multiplication satisfies the commutativity law.
For any ring 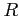 , we denote by
, we denote by 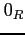 (respectively,
(respectively, 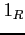 )
the zero element of
)
the zero element of 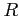 (respectively, the unit element of
(respectively, the unit element of 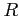 ).
Namely,
).
Namely, 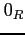 and
and 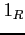 are elements of
are elements of 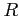 characterized by
the following rules.
characterized by
the following rules.
When no confusion arises, we omit the subscript `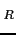 '
and write
'
and write 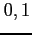 instead of
instead of 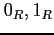 .
.
DEFINITION 01.2
A map
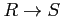
from a unital associative ring
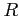
to another unital associative ring
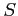
is said to be
ring homomorphism if it satisfies the following conditions.
- Ringhom-1.
-
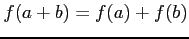
- Ringhom-2.
-
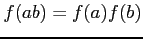
- Ringhom-3.
-
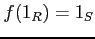
Our aim is to show the following.
THEOREM 01.3
Any regular local ring is UFD.
DEFINITION 01.4
A commutative ring
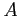
is said to be a local ring if it has only one
maximal ideal.
LEMMA 01.6
- Let
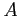 be a local ring. Then the maximal ideal of
be a local ring. Then the maximal ideal of 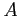 coincides with
coincides with
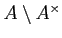 .
.
- A commutative ring
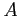 is a local ring if and only if
the set
is a local ring if and only if
the set
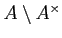 of non-units of
of non-units of 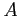 forms an ideal of
forms an ideal of 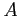 .
.



Next: Bibliography
2012-04-13
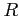 is an additive group with respect to the addition.
is an additive group with respect to the addition.
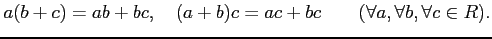
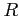 has a multiplicative unit.
has a multiplicative unit.
![]() , we denote by
, we denote by ![]() (respectively,
(respectively, ![]() )
the zero element of
)
the zero element of ![]() (respectively, the unit element of
(respectively, the unit element of ![]() ).
Namely,
).
Namely, ![]() and
and ![]() are elements of
are elements of ![]() characterized by
the following rules.
characterized by
the following rules.