![]() 行列の積、和、スカラー倍
行列の積、和、スカラー倍
(言うのをウッカリしていましたが、ベクトル空間のことを線形空間とも言います。)
ベクトル空間を比較するには線形写像を用います。
線形写像とは、和と、スカラー倍を保つような写像のことでした。
![]()
![]() から他のベクトル空間
から他のベクトル空間 ![]() への線形写像
への線形写像 ![]() は
基本ベクトルの行き先
は
基本ベクトルの行き先
![]() だけを決めれば定まるのでした。
だけを決めれば定まるのでした。
&dotfill#dotfill;
記法に関する復習と補足。
とは、
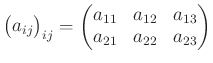
という具合である。 ここでの
行列算は世間ではよくある表計算を抽象化したものである。
答:
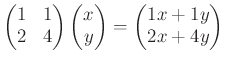
行列
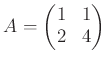 は「鶴亀行列」であり、その第一列
は「鶴亀行列」であり、その第一列
![]() は、鶴の頭と足(の個数)を、第二列
は、鶴の頭と足(の個数)を、第二列
![]() は亀の頭と足(の個数)をそれぞれ成分として並べたものである。
は亀の頭と足(の個数)をそれぞれ成分として並べたものである。
「鶴、亀」は本物の動物と言うよりは、 ギフトセットか何かの名前と思うほうがフイットするかもしれない。 「頭、足」も中の金銀や宝石のたぐいととみるとどうだろうか。
鶴亀セット。
松:
![]() (鶴 9 亀6)
竹:
(鶴 9 亀6)
竹:
![]() (鶴 8 亀5)
梅:
(鶴 8 亀5)
梅:
![]() (鶴 7 亀4)
(鶴 7 亀4)
松 ![]() セット、竹
セット、竹 ![]() セット、梅
セット、梅 ![]() セットを贈ると、
贈った鶴亀の総数は、
セットを贈ると、
贈った鶴亀の総数は、
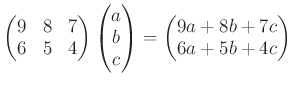
で与えられる。
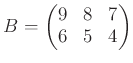 は「鶴亀セットの行列」である。
は「鶴亀セットの行列」である。
このとき「頭」と「足」の総数は
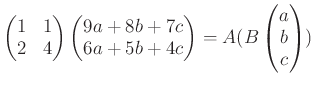
で与えられる。
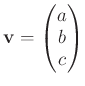 とおいて少し計算すると、この答えは、
とおいて少し計算すると、この答えは、
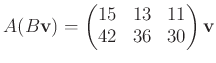
という式により新しい行列
線形写像の和。
で定義すると、
上の命題の仮定のもと、
![]() を表現する行列を
を表現する行列を ![]() ,
,
![]() を表現する行列を
を表現する行列を ![]() とおくと、
上の命題により
とおくと、
上の命題により
![]() を表現する行列が
存在するはずである。 この行列のことを
を表現する行列が
存在するはずである。 この行列のことを ![]() と書いて、行列
と書いて、行列 ![]() と
と ![]() の
和と呼ぶ。
の
和と呼ぶ。
![]() ,
,
![]() と成分で書くと、
と成分で書くと、
![]() (つまり、成分ごとの和)である。
(つまり、成分ごとの和)である。
線形写像の差、行列の差も同様にして定義される。
※レポート問題
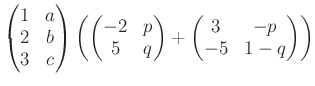
を計算せよ。