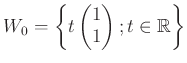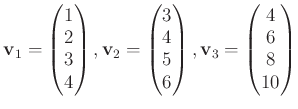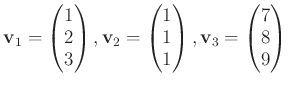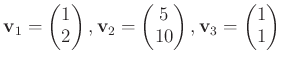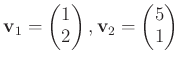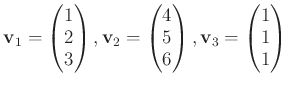Next: About this document ...
線形代数学概論 A No.2要約
 抽象的ベクトル空間、ベクトル空間の部分空間。一次独立性
抽象的ベクトル空間、ベクトル空間の部分空間。一次独立性
実数直線も、
も、「同じ形」をしている。
このような2つを同時に扱うのには、成分を見るのではなく、
和と、スカラー倍という道具のみを用いて記述することが
大事になる。例えば、成分がすべて 0
のベクトル (0
ベクトル) は
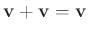 の解と見ることもできる。
そもそも、成分を扱ってばかりいるのではベクトルを研究する意味がない。
の解と見ることもできる。
そもそも、成分を扱ってばかりいるのではベクトルを研究する意味がない。
定義 2.2
ベクトル空間
の部分集合で、(同じ和とスカラー倍に関して)
ベクトル空間であるようなものを、
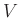
の
部分ベクトル空間と呼ぶ。
上述の 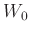 も
も
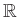
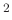 の部分ベクトル空間である。
の部分ベクトル空間である。
定義 2.3
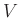
のベクトル
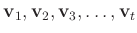
が
一次従属であるとは、
ある
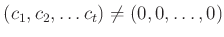
が存在して、
を満たすときにいう。
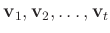
が一次従属でない場合には、
一次独立であると呼ばれる。
要するに、一次従属であるとは、与えられたベクトルの間に
関係式が存在することである。
一次独立かそうでない(一次従属)か、
は和とスカラー倍のみを用いて記述されており、
成分の値については直接は言及していない。いかにも線形代数的な概念である。
例 2.1 (線形従属なベクトルの例)
-
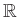
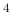 の元を
の元を
で定めると、
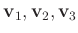 は一次従属である。
は一次従属である。
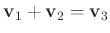 であるからである。
であるからである。
-
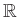
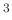 の元を
の元を
で定めると、
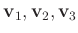 は一次従属である。
は一次従属である。
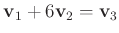 であるからである。
であるからである。
-
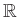
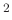 の元を
の元を
で定めると、
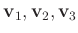 は一次従属である。
は一次従属である。
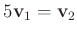 であるからである。
であるからである。
上のように、具体的な数ベクトルが一次従属であるか否かを調べるときには、
成分に言及する必要がある。
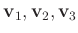 が一次従属であるという事は、
最後のベクトル
が一次従属であるという事は、
最後のベクトル
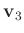 が
が
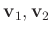 スカラー倍の和(線形結合)を用いて
書けるということにかなり近いが、最後の例のように例外も生じる。
そこで定義では最初から
スカラー倍の和(線形結合)を用いて
書けるということにかなり近いが、最後の例のように例外も生じる。
そこで定義では最初から
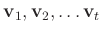 に関して
対称な形で述べてあるのである。上の(2)で言えば、
に関して
対称な形で述べてあるのである。上の(2)で言えば、
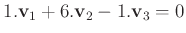 という調子である。
という調子である。
例 2.2
とおくと、
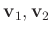
は一次独立である。
実際、
とすると、
で、これを解くと
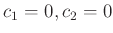
を得るからである。
線形独立性、線形従属性を判定する場合にはうえのように一次方程式に
帰着させる。下の問題も参照のこと。
※レポート問題
問題 2.1
とおくと、
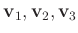
は一次独立だろうか、
それとも従属だろうか。
理由を挙げて答えなさい。



Next: About this document ...
2012-11-16
![]() 抽象的ベクトル空間、ベクトル空間の部分空間。一次独立性
抽象的ベクトル空間、ベクトル空間の部分空間。一次独立性