![]() ��ʬ��
��ʬ��
������ʬ���Ȥϡ���ʬ����Ǥ��äƷ��ˤʤäƤ����ΤΤ��ȤǤ���
����������ʬ���γݤ����Ϥ�Ȥη��γݤ����Ȱ��פ��ʤ���Фʤ�ޤ��� ��ʬ�������Τ�����ϼ��Τ褦�ˤʤ�ޤ���
�� ![]() ��Ϳ�����Ƥ���Ȥ��ޤ���
��Ϳ�����Ƥ���Ȥ��ޤ���
![]() ����ʬ����
����ʬ���� ![]() ��
�� ![]() ����ʬ���Ǥ���Ȥ�
�����ξ����������Ȥ��˸����ޤ���
����ʬ���Ǥ���Ȥ�
�����ξ����������Ȥ��˸����ޤ���
(0)�ݤ���
![]() ��
�� ![]() �����¤���ȡ�
�����
�����¤���ȡ�
����� ![]() ���ͤ���ġ����ʤ�������Τ褦�ʼ�����ͶƳ����롣
���ͤ���ġ����ʤ�������Τ褦�ʼ�����ͶƳ����롣
(1)
��� (0) �ϼ��Τ褦�˸��������Ƥ��ɤ���
(0![]() )
) ![]() ��
�� ![]() ����Ǥ�դ˼�äƤ���ȡ�
���ĤǤ�
����Ǥ�դ˼�äƤ���ȡ�
���ĤǤ� ![]() ��
�� ![]() �θ��Ǥ��롣
�θ��Ǥ��롣
�ˤ�äƷ�ޤ�ޤ����������
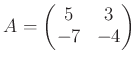
��ޤ�
�Ĥ��ν�������ܤ˺ܤäƤ��뤫���Τ�ʤ�����ɤ⡢ �����ݤ��Ĥ��ˤ��Ƥ�������Ϳ���ޤ��� �������Ƭ�˽Ҥ٤����3.1�����ȯ���ưʲ��Τλ��¤� ����Ū�������ʤ��� �����Ǥ��뤫�ɤ������ݥ���ȤǤ���