Next: About this document ...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Č―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― No.16
ïŋ―ïŋ―ïŋ―ïŋ― 16.2
ïŋ―ïŋ―ïŋ―ïŋ―
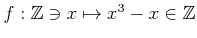
ïŋ―ËĪÄĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĄĢïŋ―ïŋ―ïŋ―ėĪūïŋ―ïŋ―ïŋ―ïŋ―Íģïŋ―ïŋ―ŌĪŲĪëĪģïŋ―ČĄïŋ―
-
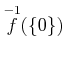 ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
-
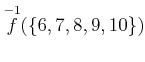 ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―
16.1
(1) P ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
(2) P ïŋ―ÎĪÛĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
[ïŋ―ïŋ―ïŋ―ïŋ―]
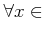
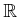
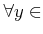
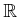 ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÞĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÞĄïŋ― 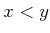 ïŋ―Čēïŋ―ïŋ―ęĪđïŋ―ïŋ―ČĄïŋ―
ïŋ―Čēïŋ―ïŋ―ęĪđïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
 ïŋ―ïŋ―[ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―]
ïŋ―ïŋ―[ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―]
(
 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―âĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÜĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―âĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÜĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ)
16.2
(1)
(2)
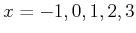 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 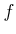 ïŋ―ïŋ―ïŋ―ÍĪÏĪïŋ―ïŋ―ėĪūïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÍĪÏĪïŋ―ïŋ―ėĪūïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ęĄĒ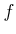 ïŋ―ïŋ―
ïŋ―ïŋ― 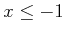 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ÃĪĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ÃĪĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ
Æąïŋ―ÍĪËĄïŋ―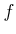 ïŋ―ïŋ―
ïŋ―ïŋ― 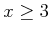 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ÃĪĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ÃĪĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ
ïŋ―æĪĻïŋ―ËĄïŋ―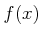 ïŋ―ïŋ―ïŋ―ÍĪïŋ―
ïŋ―ïŋ―ïŋ―ÍĪïŋ―
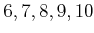 ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ėĪŦïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
(
ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ėĪŦïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
(
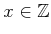 ïŋ―Îūïŋ―ïŋ―ÎĪïŋ―ČĪïŋ―)
ïŋ―Îūïŋ―ïŋ―ÎĪïŋ―ČĪïŋ―) 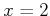 ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ËļÂĪëĄĢïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ËļÂĪëĄĢïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
2011-08-04
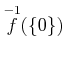 ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
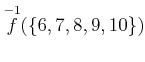 ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ