- P ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ėŋïŋ―ïŋ― (not P)ïŋ―ïŋ―ïŋ―not ïŋ―ïŋ―ČĪïĪšïŋ―ËĄŨ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- P ïŋ―ïŋ― not P ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ÎĪÏĪÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―15ïŋ―ïŋ―ïŋ―ÜĪΞïŋ―ïŋ―ïŋ― : ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
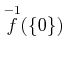 ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
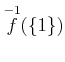 ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
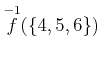 ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪëĄĢïŋ―ïŋ―ïŋ―ïŋ―
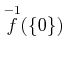 ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
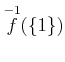 ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪëĄĢïŋ―ïŋ―ïŋ―ïŋ―