


Next: About this document ...
пњљпњљпњљпњљпњљ»љпњљпњљпњљпњљпњљпњљпњљ No.13
пњљпњљ13пњљпњљпњљ№§ќЉпњљпњљпњљ :

пњљпњљпњљ 13.1 (пњљпњљ)
пњљпњљпњљпњљ
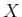
пњљпњљпњљпњљ ђпњљпњљпњљпњљпњљ¬≤
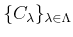
пњљпњљ
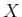
пњљпњљ
пњљпњљпњљй•є ђпњљпњљ (
ђпњљпњљпњљ»§пњљпњљпњљпњљ)пњљ«§пњљпњљпњљ»§ѕ°пњљпњљƒ§пњљпњљќ§пњљпњљ»§пњљпњљпњљпњљпњљќ©пњљƒ§»§пњљпњљЋЄпњљпњљпњљпњљпњљ
-
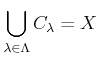 .
.
-
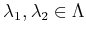 ,
,
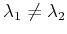 пњљ §пњљпњљ
пњљ §пњљпњљ
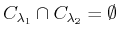 .
.
пњљпњљ∆±пњљЌіЎЈпњљпњљ„§»°пњљпњљпњљпњљпњљпњљ«Єпњљпњљпњљпњљ»§пњљпњљпњљпњљќ°пњљ∆±пњљЌ°„§»§пњљ
(пњљпњљпњљќњпњљпњљћ§пњљпњљй§§пњљЋ§ѕ§пњљпњљпњљпњљл§ђ)пњљпњљпњљпњљ ™пњљ«§пњљпњљл°£пњљи§ѓпњљпњљпњљћ§пњљпњљл§≥пњљ»°пњљ
пњљпњљпњљпњљ 13.1 (пњљпњљ)
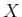
пњљќ•пњљпњљй•є ђпњљпњљ
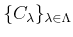
пњљпњљЌњпњљпњљпњљпњљм§њпњљ»§пњљпњљпњљ
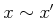
пњљ«§пњљпњљл§≥пњљ»§пњљ
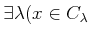
and
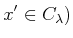
пњљпњљпњљЁ§пњљпњљпњљ»љпњљк§єпњљпњљ–°пњљпњљпњљпњљпњљ
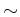
пњљпњљ∆±пњљЌіЎЈпњљпњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 13.2 (пњљпњљ)
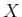
пњљпњљ∆±пњљЌіЎЈпњљ
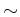
пњљпњљЌњпњљпњљпњљпњљпњљ∆§пњљпњљпњљ»§пњљпњљл°£
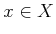
пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљ»§пњљпњљпњљпњљ»§пњљпњљпњљпњљпњљпњљќ§пњљпњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
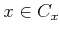 . пњљ»§пњљпњљЋ°пњљ
. пњљ»§пњљпњљЋ°пњљ
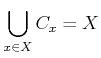 .
.
-
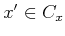
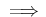
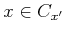 .
.
-
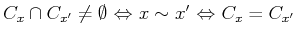 .
.
пњљпњљџ§…§пњљ∆±пњљЌ§Ћ°пњљ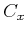 пњљќ§ §пњљпњљпњљпњљпњљпњљ £пњљпњљпњљпњљпњљќ§пњљ §пњљпњљпњљпњљ»§Ћ§пњљк°Ґ
пњљќ§ §пњљпњљпњљпњљпњљпњљ £пњљпњљпњљпњљпњљќ§пњљ §пњљпњљпњљпњљ»§Ћ§пњљк°Ґ
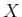 пњљќ•пњљпњљй•є ђпњљпњљпњљпњљпњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљ∆∞„§пњљ ђпњљпњљпњљпњљи§¶пњљЋ°пњљпњљеµ≠2пњљпњљпњљпњљпњљпњљпњљпњљѕЄя§пњљпњљЋµ’§Ћ§ §√§∆§пњљпњљл°£
пњљпњљпњљ §пњљпњљпњљпњљпњљпњљпњљй•є ђпњљпњљпњљпњљЌњпњљпњљпњљл§≥пњљ»§»§пњљ∆±пњљЌіЎЈпњљпњљпњљЌњпњљпњљпњљл§≥пњљ»§пњљ
пњљ№Љпњљ≈™пњљпњљ∆±пњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљќ•пњљпњљй•є ђпњљпњљпњљпњљпњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљ∆∞„§пњљ ђпњљпњљпњљпњљи§¶пњљЋ°пњљпњљеµ≠2пњљпњљпњљпњљпњљпњљпњљпњљѕЄя§пњљпњљЋµ’§Ћ§ §√§∆§пњљпњљл°£
пњљпњљпњљ §пњљпњљпњљпњљпњљпњљпњљй•є ђпњљпњљпњљпњљЌњпњљпњљпњљл§≥пњљ»§»§пњљ∆±пњљЌіЎЈпњљпњљпњљЌњпњљпњљпњљл§≥пњљ»§пњљ
пњљ№Љпњљ≈™пњљпњљ∆±пњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљ 13.3
пњљпњљпњљпњљ
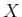
пњљпњљ∆±пњљЌіЎЈпњљ
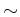
пњљпњљЌњпњљпњљпњљпњљпњљ∆§пњљпњљпњљ»§пњљпњљпњљ
пњљпњљпњљпњљ
13.2 пњљ«Єпњљпњљпњљпњљи§¶пњљпњљ
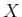
пњљЋЉпњљпњљќ§и§¶пњљ •пњљпњљй•є ђпњљпњљпњљпњљпњљпњљё§пњљќ§«§пњљпњљ√§пњљпњљпњљ
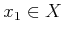
пњљпњљ
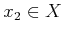
пњљ»§пњљ∆±пњљпњљпњљпњљпњљй•є
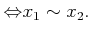
пњљпњљпњљќ•пњљпњљй•є ђпњљпњљпњљЋ§пњљл•ѓпњљй•єпњљпњљпњљпњљпњљќ§пњљ
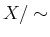
пњљ»§пњљ”°пњљ
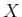
пњљпњљ
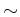
пњљЋ§пњљпњљ
пњљпњљпњљпњљпњљпњљпњљ»§пњљ÷°пњљ
пњљпњљпњљпњљ 13.3 (пњљпњљ)
пњљпњљпњљпњљ
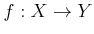
пњљпњљЌњпњљпњљпњљпњљпњљ∆§пњљпњљпњљ»§пњљпњљпњљ
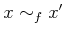
пњљпњљпњљЁ§пњљпњљпњљ»љпњљпњљпњљ
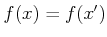
пњљпњљпњљЁ§пњљпњљ«§пњљпњљпњљ»§пњљпњљпњљ
пњљпњљпњљ §пњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљ»§пњљпњљпњљ
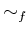
пњљпњљ
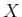
пњљпњљ∆±пњљЌіЎЈпњљпњљ«§пњљпњљл§≥пњљ»§пњљ
пњљпњљпњљпњљЋљпњљпњљ√§∆Љпњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљ 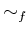 пњљпњљ ≤пњљпњљ«§пњљќЃпњљ—§пњљпњљл°£
пњљпњљ ≤пњљпњљ«§пњљќЃпњљ—§пњљпњљл°£



Next: About this document ...
2011-07-13
![]()
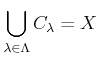 .
.
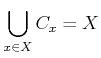 .
.
![]() пњљќ§ §пњљпњљпњљпњљпњљпњљ £пњљпњљпњљпњљпњљќ§пњљ §пњљпњљпњљпњљ»§Ћ§пњљк°Ґ
пњљќ§ §пњљпњљпњљпњљпњљпњљ £пњљпњљпњљпњљпњљќ§пњљ §пњљпњљпњљпњљ»§Ћ§пњљк°Ґ
![]() пњљќ•пњљпњљй•є ђпњљпњљпњљпњљпњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљ∆∞„§пњљ ђпњљпњљпњљпњљи§¶пњљЋ°пњљпњљеµ≠2пњљпњљпњљпњљпњљпњљпњљпњљѕЄя§пњљпњљЋµ’§Ћ§ §√§∆§пњљпњљл°£
пњљпњљпњљ §пњљпњљпњљпњљпњљпњљпњљй•є ђпњљпњљпњљпњљЌњпњљпњљпњљл§≥пњљ»§»§пњљ∆±пњљЌіЎЈпњљпњљпњљЌњпњљпњљпњљл§≥пњљ»§пњљ
пњљ№Љпњљ≈™пњљпњљ∆±пњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљќ•пњљпњљй•є ђпњљпњљпњљпњљпњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљ∆∞„§пњљ ђпњљпњљпњљпњљи§¶пњљЋ°пњљпњљеµ≠2пњљпњљпњљпњљпњљпњљпњљпњљѕЄя§пњљпњљЋµ’§Ћ§ §√§∆§пњљпњљл°£
пњљпњљпњљ §пњљпњљпњљпњљпњљпњљпњљй•є ђпњљпњљпњљпњљЌњпњљпњљпњљл§≥пњљ»§»§пњљ∆±пњљЌіЎЈпњљпњљпњљЌњпњљпњљпњљл§≥пњљ»§пњљ
пњљ№Љпњљ≈™пњљпњљ∆±пњљпњљпњљпњљпњљ«§пњљпњљл°£
![]() пњљпњљ ≤пњљпњљ«§пњљќЃпњљ—§пњљпњљл°£
пњљпњљ ≤пњљпњљ«§пњљќЃпњљ—§пњљпњљл°£