


Next: About this document ...
�����Ƚ������� No.10
��10���ܤμ��� :

��� 10.1 (��)
�¿�
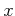
���Ф��ơ�
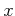
��Ķ���ʤ��褦�������Τ�������Τ�Τ�
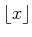
�Ƚ�(floor of
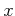
���ɤࡣ)��
�㤨�С�
�Ǥ��롣�ޤ���Ǥ�դ�����
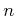
���Ф��ơ�
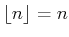
�Ǥ��롣
���� 10.1 (��)
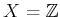
,
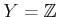
�Ȥ�����
����
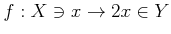
��
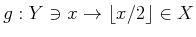
�ˤ������ơ�
-
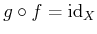 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
-
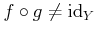 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
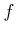 ,
, 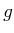 �Ϥ��줾�����͡�ñ�͡���ñ�ͤ���������
�Ϥ��줾�����͡�ñ�͡���ñ�ͤ���������
�����Τ褦�ˡ�
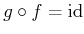 ���������Ȥ���
���������Ȥ���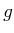 ��
�� 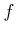 �����ռ�����
����Ȥ�����(
�����ռ�����
����Ȥ�����(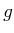 ����ߤ��
����ߤ�� 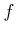 ��
�� 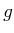 �����ռ����Ǥ��롣���ΤȤ���
����9.2�η�̤ˤ�ꡢ
�����ռ����Ǥ��롣���ΤȤ���
����9.2�η�̤ˤ�ꡢ
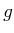 �����ͤ�
�����ͤ� 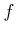 ��ñ�ͤǤ���Τ��狼�뤳�Ȥ����դ��Ƥ�������
)
��ñ�ͤǤ���Τ��狼�뤳�Ȥ����դ��Ƥ�������
)
���� 10.2
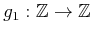
��
����������
����
10.1 ��
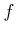
����
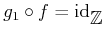
������Ω�Ĥ��Ȥ��ʤ�����
���� 10.3
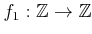
��
����������
����
10.1 ��
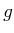
����
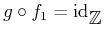
������Ω�Ĥ��Ȥ��ʤ�����
���� 10.4 (��)
![$ X={\mathbb{C}}[t] $](img22.png)
(ʣ�ǿ�������
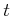
���ѿ��Ȥ���¿�༰�����ΤΤʤ�����),
![$ Y={\mathbb{C}}[t]$](img24.png)
�Ȥ�����
����
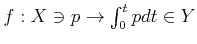
��
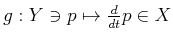
�ˤ������ơ�
-
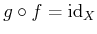 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
-
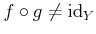 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
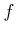 ,
, 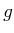 �Ϥ��줾�����͡�ñ�͡���ñ�ͤ���������
�Ϥ��줾�����͡�ñ�͡���ñ�ͤ���������

��� 10.2
����
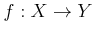
��Ϳ�����Ƥ���Ȥ���
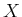 ����ʬ����
����ʬ���� 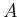 ���Ф��ơ�����
���Ф��ơ����� 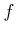 �ˤ��
��(�����Ȥ����)
�ˤ��
��(�����Ȥ����) 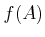 ��
��
��������롣
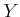 ����ʬ����
����ʬ���� 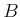 ���Ф��ơ�����
���Ф��ơ����� 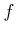 �ˤ������
�ˤ������
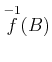 ��
��
�ˤ��������롣
�ռ�����Ʊ������
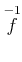 ��ȤäƤ��뤱��ɤ⡢
��������
��ȤäƤ��뤱��ɤ⡢
����ε����� 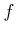 �εռ�����¸�ߤ��ʤ����ˤ����Ƥ���������
�Ȥ������Ȥ�
���դ��Ƥ�������
�εռ�����¸�ߤ��ʤ����ˤ����Ƥ���������
�Ȥ������Ȥ�
���դ��Ƥ�������
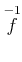 ��(�������ˤ�餺)������Ū�ˤϻȤ��䤹����
�Ĥޤꡢ
��(�������ˤ�餺)������Ū�ˤϻȤ��䤹����
�Ĥޤꡢ
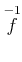 �Ϥ��ޤ��ޤʽ��绻�ȲĴ��Ǥ��롣
�Ϥ��ޤ��ޤʽ��绻�ȲĴ��Ǥ��롣
���� 10.5 �Ǹ����褦�ˡ�
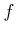 �����ˤĤ��Ƥϵ����ۤɤʤ�Ǥ⥢��Ȥ����櫓�ˤϤ����ʤ���
�ܤ����Ͻ��������ܤ�Ф褤����
���������äƤϼ��㤬���줿���ˤ������ٹͤ��뤰�餤��
��ʬ��������
�����ˤĤ��Ƥϵ����ۤɤʤ�Ǥ⥢��Ȥ����櫓�ˤϤ����ʤ���
�ܤ����Ͻ��������ܤ�Ф褤����
���������äƤϼ��㤬���줿���ˤ������ٹͤ��뤰�餤��
��ʬ��������



Next: About this document ...
2011-06-22
![]()
![]()
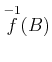 ��
��
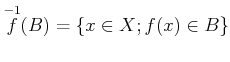
![]() ��ȤäƤ��뤱��ɤ⡢
��������
��ȤäƤ��뤱��ɤ⡢
����ε����� ![]() �εռ�����¸�ߤ��ʤ����ˤ����Ƥ���������
�Ȥ������Ȥ�
���դ��Ƥ�������
�εռ�����¸�ߤ��ʤ����ˤ����Ƥ���������
�Ȥ������Ȥ�
���դ��Ƥ�������
![$ \overset{-1}{f}([1,2]) $](img47.png) ����衣
����衣
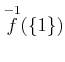 ����衣
����衣
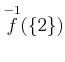 ����衣
����衣
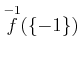 ����衣
����衣
![$ \overset{-1}{f}([-2,-1]) $](img51.png) ����衣
����衣
![$ \overset{-1}{f} ([1,2]\cup [3,4])$](img52.png) ����衣
����衣
![]() ��(�������ˤ�餺)������Ū�ˤϻȤ��䤹����
�Ĥޤꡢ
��(�������ˤ�餺)������Ū�ˤϻȤ��䤹����
�Ĥޤꡢ
![]() �Ϥ��ޤ��ޤʽ��绻�ȲĴ��Ǥ��롣
�Ϥ��ޤ��ޤʽ��绻�ȲĴ��Ǥ��롣
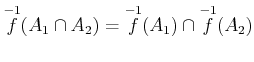 .
.
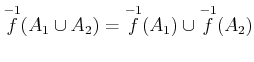 .
.
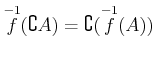 .
.
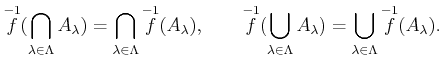
![]() �����ˤĤ��Ƥϵ����ۤɤʤ�Ǥ⥢��Ȥ����櫓�ˤϤ����ʤ���
�ܤ����Ͻ��������ܤ�Ф褤����
���������äƤϼ��㤬���줿���ˤ������ٹͤ��뤰�餤��
��ʬ��������
�����ˤĤ��Ƥϵ����ۤɤʤ�Ǥ⥢��Ȥ����櫓�ˤϤ����ʤ���
�ܤ����Ͻ��������ܤ�Ф褤����
���������äƤϼ��㤬���줿���ˤ������ٹͤ��뤰�餤��
��ʬ��������