


Next: About this document ...
�����Ƚ������� No.9
��9���ܤμ��� :

���� 9.1 (��)
����
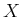
,
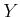
��Ϳ�����Ƥ���Ȥ��롣
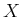
�Τ��Τ��Τθ�
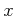
������
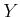
�Υ��ԡ�
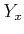
���Ѱդ���С�
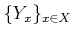
�ϤҤȤĤν����²�Ǥ��롣
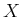
����
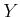
�ؤμ���
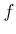
��
�θ�
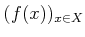
��Ʊ��뤵��롣���ʤ����
ľ�ѽ���
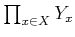
��
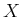
����
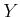
�ؤμ������Τν����Ʊ���Ǥ��롣
��� 9.2 (��)
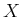
����
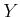
�ؤμ��������ΤΤʤ������
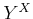
�Ƚ�����Ϥޤ�
�Ƚ��⤢�롣
���� 9.3 (��)
���Ǥʤ�����Ф��꤫��ʤ뽸��²
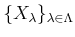
��
�������ơ�
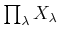
�϶��ǤϤʤ���
����������ȡ�̵�¸Ĥζ��Ǥʤ����礿��
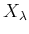
���顢���ä����˰�ĤŤ�
������Ф����Ȥ���ǽ�Ǥ��롣
���֥ۥƥ�ҥ�٥�ȡ�
���̤ˡ� 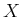 ����
���� 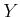 �ؤ�ñ�ͤ�¸�ߤ��뤳�Ȥϡ�
�ؤ�ñ�ͤ�¸�ߤ��뤳�Ȥϡ�
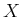 �θ��Τۤ���
�θ��Τۤ��� 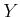 �θ�����־��ʤ��פ��Ȥ��̣����ȹͤ����롣
�θ�����־��ʤ��פ��Ȥ��̣����ȹͤ����롣
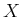 �γơ��θ���ֿ͡ס�
�γơ��θ���ֿ͡ס�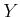 �γơ��θ���֥ۥƥ�������פ��㤨��ȡ�
ñ�ͤ�¸�ߤϰ�ͤҤȤ꤬�̡�������������뤳�Ȥ��̣���뤫��Ǥ��롣
��������̵�½���ˤ����Ƥϡ���¿���ס־��ʤ��פδ��Ф�ͭ�½���Ȥ�
�����ۤʤ롣
�γơ��θ���֥ۥƥ�������פ��㤨��ȡ�
ñ�ͤ�¸�ߤϰ�ͤҤȤ꤬�̡�������������뤳�Ȥ��̣���뤫��Ǥ��롣
��������̵�½���ˤ����Ƥϡ���¿���ס־��ʤ��פδ��Ф�ͭ�½���Ȥ�
�����ۤʤ롣
���� 9.4 (��)
����
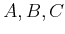
���Ф��ơ�
���ʤꤿ�ġ�
���� 9.5 (�٥�奿����,��)
���ʤꤿ�ġ�
ǻ�٤θ���(�ȥ٥�奿���������)���Ѥ���ȡ����Τ��Ȥ�ʬ����
�������
��� 9.6
����
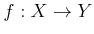
��
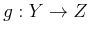
��Ϳ�����Ƥ���Ȥ��롣
���ΤȤ���
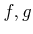
�������
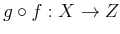
��
��������롣
��� 9.7
����
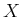
���Ф��ơ�����
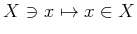
��
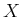
��
���������Ȥ�����
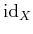
��ɽ����
��� 9.8
�¿�
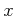
���Ф��ơ�
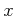
��Ķ���ʤ��褦�������Τ�������Τ�Τ�
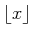
�Ƚ�(floor of
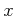
���ɤࡣ)��
�㤨�С�
�Ǥ��롣�ޤ���Ǥ�դ�����
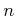
���Ф��ơ�
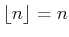
�Ǥ��롣
���̤ˡ��¿� 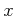 ������
������ 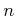 ���Ф��ơ�
���Ф��ơ�
�ˤ����դ��Ƥ��������Τ�
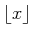 �Τ��Ȥ�
�Τ��Ȥ� ![$ [x]$](img49.png) ��
�ơ��֥���������פȸƤ֤��Ȥ�¿���ä�����
���� floor �Τۤ����̤꤬�ɤ��ʤ�ĤĤ���褦�Ǥ��롣
��
�ơ��֥���������פȸƤ֤��Ȥ�¿���ä�����
���� floor �Τۤ����̤꤬�ɤ��ʤ�ĤĤ���褦�Ǥ��롣
���� 9.4
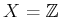
,
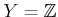
�Ȥ�����
����
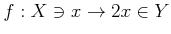
��
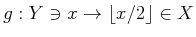
�ˤ������ơ�
-
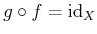 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
-
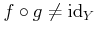 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
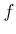 ,
, 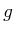 �Ϥ��줾�����͡�ñ�͡���ñ�ͤ���������
�Ϥ��줾�����͡�ñ�͡���ñ�ͤ���������
���� 9.5
![$ X={\mathbb{C}}[t] $](img55.png)
(ʣ�ǿ�������
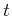
���ѿ��Ȥ���¿�༰�����ΤΤʤ�����),
![$ Y={\mathbb{C}}[t]$](img57.png)
�Ȥ�����
����
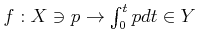
��
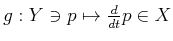
�ˤ������ơ�
-
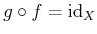 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
-
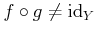 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
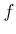 ,
, 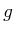 �Ϥ��줾�����͡�ñ�͡���ñ�ͤ���������
�Ϥ��줾�����͡�ñ�͡���ñ�ͤ���������



Next: About this document ...
2011-06-14
![]()
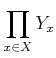
![]() ����
���� ![]() �ؤ�ñ�ͤ�¸�ߤ��뤳�Ȥϡ�
�ؤ�ñ�ͤ�¸�ߤ��뤳�Ȥϡ�
![]() �θ��Τۤ���
�θ��Τۤ��� ![]() �θ�����־��ʤ��פ��Ȥ��̣����ȹͤ����롣
�θ�����־��ʤ��פ��Ȥ��̣����ȹͤ����롣
![]() �γơ��θ���ֿ͡ס�
�γơ��θ���ֿ͡ס�![]() �γơ��θ���֥ۥƥ�������פ��㤨��ȡ�
ñ�ͤ�¸�ߤϰ�ͤҤȤ꤬�̡�������������뤳�Ȥ��̣���뤫��Ǥ��롣
��������̵�½���ˤ����Ƥϡ���¿���ס־��ʤ��פδ��Ф�ͭ�½���Ȥ�
�����ۤʤ롣
�γơ��θ���֥ۥƥ�������פ��㤨��ȡ�
ñ�ͤ�¸�ߤϰ�ͤҤȤ꤬�̡�������������뤳�Ȥ��̣���뤫��Ǥ��롣
��������̵�½���ˤ����Ƥϡ���¿���ס־��ʤ��פδ��Ф�ͭ�½���Ȥ�
�����ۤʤ롣
![]() ������
������ ![]() ���Ф��ơ�
���Ф��ơ�