пњљпњљ5пњљпњљпњљ№§ќЉпњљпњљпњљ :
![]()
пњљпњљпњљ—љпњљпњљпњљ
пњљпњљ
пњљпњљ√§»∞пњљпњљћ§Ћ°пњљ
пњљпњљ
пњљ—љпњљпњљпњљѕ°пњљпњљ—§ќљпњљпњљпњљ„§«§пњљпњљ §пњљпњљпњљпњљпњљпњљќ§пњљпњљ»§пњљƒіпњљпњљпњљл§њпњљб°Ґ пњљ—љпњљпњљпњљќ§пњљпњљ»§пњљ÷•«•пњљпњљпњљпњљпњљ—љпњљпњљпњљ„§»§пњљпњљ÷љпњљпњљпњљ»§пњљпњљ∆§пњљƒЊпњљ—°„§»Є∆§÷§пњљпњљ»§в§Ґпњљл°£
![]()
![]()
![]() пњљќ§пњљпњљ»§пњљ
пњљќ§пњљпњљ»§пњљ
![]()
![]() ,
,
![]()
![]()
![]() пњљќ§пњљпњљ»§пњљ
пњљќ§пњљпњљ»§пњљ
![]()
![]() пњљпњљпњљпњљ
ќђпњљпњљпњљпњљпњљл°£
пњљпњљпњљпњљ
ќђпњљпњљпњљпњљпњљл°£
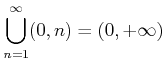
пњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
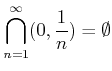
пњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
![$\displaystyle \bigcap_{\epsilon>0} (-\infty, 1+\epsilon) =(-\infty, 1]
$](img42.png)
пњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ пњљпњљпњљпњљпњљпњљпњљпњљпњљ4.8 пњљпњљпњљпњљ”§пњљпњљќ•пњљпњљпњљпњљ»§ѕі÷∞пњљ√§∆§пњљпњљпњљ. пњљеµ≠пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ(Web пњљ«§ѕљпњљпњљпњљпњљ—§пњљ).
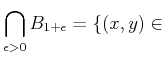
пњљпњљпњљпњљпњљпњљќ©пњљƒ§пњљпњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ