ïŋ―ïŋ―2ïŋ―ïŋ―ïŋ―ÜĪΞïŋ―ïŋ―ïŋ― :
![]()
ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―(Âģïŋ―ïŋ―)
ïŋ―ïŋ―![]() ïŋ―ĘĪïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ― ![]() ïŋ―ŨĪÏĄïŋ―
ïŋ―ŨĪÏĄïŋ―![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪČĪïŋ―ïŋ―ËĪÏĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪČĪïŋ―ïŋ―ËĪÏĄïŋ―![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪïŋ―ïŋ―ČĪïŋ―
ïŋ―ïŋ―ÄĨïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢïŋ―ĮĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪïŋ―ïŋ―ČĪïŋ―
ïŋ―ïŋ―ÄĨïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢïŋ―ĮĪïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ČĪïŋ―ïŋ―ËĪÏĪÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪÏūïŋ―ïŋ―Ëąïŋ―ïŋ―ïŋ―ïŋ―Æžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪΰïŋ―ĖĢïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ČĪïŋ―ïŋ―ËĪÏĪÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪÏūïŋ―ïŋ―Ëąïŋ―ïŋ―ïŋ―ïŋ―Æžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪΰïŋ―ĖĢïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
![]() ïŋ―ÏĄïŋ―
ïŋ―ÏĄïŋ― ![]() ïŋ―ïŋ―ïŋ―ęĪđïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ęĪđïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ŨĪČēïŋ―áĪđïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪÏĄïŋ―ïŋ―ïŋ―ïŋ―ëēūïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ŨĪČēïŋ―áĪđïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪÏĄïŋ―ïŋ―ïŋ―ïŋ―ëēūïŋ―ïŋ― ![]() ïŋ―ōĪŠĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ËĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―§ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ōĪŠĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ËĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―§ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―Æģïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―Âūïŋ―ĘĪïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Æģïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―Âūïŋ―ĘĪïŋ―ĘĪïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―Îŋïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪĮĪïŋ―ïŋ―ïŋ―ŨĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―Îŋïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪĮĪïŋ―ïŋ―ïŋ―ŨĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ČĪïŋ―
Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―
Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―Č―ņĪŊĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―(
ïŋ―Č―ņĪŊĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―(
![]() ) ïŋ―ïŋ―ïŋ―ïŋ― (
) ïŋ―ïŋ―ïŋ―ïŋ― (
![]() )ïŋ―ïŋ― ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪĮĪïŋ―ïŋ―ëĄĢ
)ïŋ―ïŋ― ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪĪïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―Îīïŋ―ïŋ―ïŋ―ÅŠïŋ―Ęŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―§ïŋ―âĄĒïŋ―ïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―Äūïŋ―ïŋ―ïŋ―ïŋ― Æģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ãĪĻïŋ―Оïŋ―ïŋ―ÎĪčĪĶïŋ―Ęķïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ïŋ―°ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―°ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―
ïŋ―ņĪĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪĘĪïŋ―ïŋ―ČĪïŋ―
ïŋ―ïŋ―
ïŋ―ņĪĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪĘĪïŋ―ïŋ―ČĪïŋ― ![]() ïŋ―ČĪïŋ―
ïŋ―ČĪïŋ―
![]() ïŋ―Č―ņĪŊĄïŋ―
ïŋ―Č―ņĪŊĄïŋ―
ïŋ―ïŋ―ïŋ―ČĪÎĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆīÞĪÞĪïŋ―ïŋ―ŨĪČĪÎķïŋ―ïŋ―ĖĪïŋ―Äīïŋ―ïŋ―ïŋ―ëĪŋïŋ―áĄĒ
![]() ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―
ïŋ―ïŋ―
ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―
ïŋ―ïŋ― ![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―Ëļïŋ―ïŋ―ČĪïŋ―ïŋ―ÆīÞĪÞĪïŋ―ëĄĢïŋ―ŨĪČĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ōĪđĪëĪģïŋ―ČĪâĪĒïŋ―ëĄĢ
ïŋ―Ëļïŋ―ïŋ―ČĪïŋ―ïŋ―ÆīÞĪÞĪïŋ―ëĄĢïŋ―ŨĪČĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ōĪđĪëĪģïŋ―ČĪâĪĒïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―æĨŦïŋ―ÃĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ë―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ÕĪĮĄïŋ―ïŋ―ïŋ―ïŋ―ëĪĪïŋ―ÏĨęĨđïŋ―ČĨïŋ―ïŋ―ÃĨŨĪïŋ―ïŋ―ïŋ― ïŋ―ņĪĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōļŦĪčĄĢ
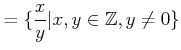 .
.
ïŋ―ãĪĻïŋ―Ðūïŋ―ïŋ―(3)ïŋ―ÎĪčĪĶïŋ―ËĄïŋ―![]() ïŋ―Ξïŋ―
ïŋ―Ξïŋ― ![]() ïŋ―ČĄïŋ―
ïŋ―ČĄïŋ― ![]() ïŋ―ïŋ―
ïŋ―Ņŋïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―Ėŋïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―Ņŋïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―Ėŋïŋ―ïŋ― ![]() ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ĘĪë―ļïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ĘŽïŋ―ïŋ―ĘŽïŋ―ØĪĮŧČĪïŋ―ïŋ―Öķïŋ―ÖĄŨĪËĪÄĪïŋ―ïŋ―ÆĪïŋ―ņĪĪĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ÄĪÎ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ËĪÏĄïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ËĪÏĄïŋ―
ïŋ―ïŋ―![]() ïŋ―ïŋ― ïŋ―ïŋ― ïŋ―ïŋ―
ïŋ―ïŋ― ïŋ―ïŋ― ïŋ―ïŋ―![]() ïŋ―ïŋ― ïŋ―ČĪïŋ―Æąïŋ―ÍĪĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―Æŧïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ― ïŋ―ČĪïŋ―Æąïŋ―ÍĪĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―Æŧïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ÃĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪÏŧČĪÃĪÆĪïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
(
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Čūïŋ―Į―ŌĪŲĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ĘŽïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆđÍĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―
ïŋ―ōĪ―ĪėĪūïŋ―ïŋ―
![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―ÃĨïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÃĨïŋ― ![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―![]() ïŋ―ïŋ―ïŋ―óĨŋĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―óĨŋĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ÉĪāĄĢïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÉĪāĄĢïŋ―ïŋ―![]() ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ÉĪïŋ―ÍĪâĪĪïŋ―ĘĪïŋ―ïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―Ęķïŋ―ïŋ―ïĪ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÛĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―Æąïŋ―ÍĪËĄïŋ―
ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ÉĪïŋ―ÍĪâĪĪïŋ―ĘĪïŋ―ïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―Ęķïŋ―ïŋ―ïĪ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÛĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―Æąïŋ―ÍĪËĄïŋ―
![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ÃĨïŋ―
ïŋ―ïŋ―ïŋ―ÃĨïŋ― ![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―![]() ïŋ―ïŋ―ËĨïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ËĨïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ÉĪāĄĢ
ïŋ―ïŋ―ïŋ―ÉĪāĄĢ
ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ηïŋ―ĖĪïŋ―ïŋ―éĪđïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ëĄĢ