![]()
ïŋ―ïŋ―
![]()
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŨĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŨĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
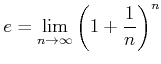
ïŋ―ÕīØŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ęĄĒ![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ïŋ―ÏĒÂģïŋ―Øŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―
ïŋ―ïĪŦïŋ―ëĄĢ
ïŋ―ïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ïŋ―ÏĒÂģïŋ―Øŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―
ïŋ―ïĪŦïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ØĪĮĪïŋ―ïŋ―ĮĪïŋ―ĘĪïŋ―ïŋ―ÂĪïŋ―ïŋ―Ðŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ― ![]() ïŋ―ïŋ―ČĪęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ðŋïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ĖĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ČĪęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ðŋïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ĖĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―Îĩïŋ―Æ°ïŋ―ōĩ―ŌĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Îĩïŋ―Æ°ïŋ―ōĩ―ŌĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ÎĪČĪïŋ―ïŋ―Îĩïŋ―Æ°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÎĪČĪïŋ―ïŋ―Îĩïŋ―Æ°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
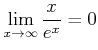
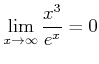
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
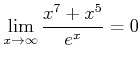
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―
![]()
![]() ïŋ―ïŋ―ÏĒÂģïŋ―ĘĪïŋ―ïŋ―
ïŋ―ïŋ―ÏĒÂģïŋ―ĘĪïŋ―ïŋ―
![]()
![]() ïŋ―ïŋ―
ïŋ―ïŋ―
![]()
![]() ïŋ―ïŋ―ÏĒÂģïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ÏĒÂģïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪÏĄïŋ―ïŋ―ÄĪïŋ―ïŋ―ÎĪčĪĶïŋ―ĘĪïŋ―ïŋ―ČĪïŋ―ČĪïŋ―ïŋ―Ðđïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ÆĨïŋ―ïŋ―ÃĨïŋ―ïŋ―ęĪđïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―12.1 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ĮĪïŋ―ÕĪïŋ―
![]() ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
( ![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ÃĪÆĄïŋ―
ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ÃĪÆĄïŋ―
![]() ïŋ―ïŋ―ïŋ―įĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îŋïŋ―ïŋ―ÛĪōĪ·ĪĘĪïŋ―ïŋ―ÆšŅĪāĄĢ)
ïŋ―ïŋ―ïŋ―įĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îŋïŋ―ïŋ―ÛĪōĪ·ĪĘĪïŋ―ïŋ―ÆšŅĪāĄĢ)
![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―
ïŋ―ïŋ―
![]() ïŋ―ČĪĘĪïŋ―čĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ČĪĘĪïŋ―čĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―

![]() ïŋ―ïŋ―
ïŋ―ïŋ―
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―ĮĪïŋ―ÕĪïŋ―Íïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―čĪĶïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―ĮĪïŋ―ÕĪïŋ―Íïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―čĪĶïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
No.12 ïŋ―ÎđÖĩïŋ―ïŋ―ïŋ―Ë―ŌĪŲĪïŋ―ïŋ―čĪĶïŋ―ËĄïŋ―
Âūïŋ―ïŋ―ïŋ―ĮĄïŋ―
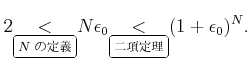
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―Ïŋïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ĮžËĄïŋ―Îĩïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―) ïŋ―æĪĻïŋ―ËĄïŋ―
(14.1), (14.2), (14.3) ïŋ―ïŋ―ïŋ―ČĪßđïŋ―ïĪŧïŋ―ëĪģïŋ―ČĪËĪïŋ―ęĄĒ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïĪŦïŋ―ëĄĢ ![]() ARRAY(0x8edbfa0)
ARRAY(0x8edbfa0)