


Next: About this document ...
��ʬ��ʬ�س���AI���� No.12

��� 12.1 (``§3 (I)(p.18)'')
�¿��Τ�����
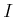
��������줿�ؿ�
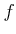
������ñĴ���ôؿ��Ǥ���Ȥϡ�
��ߤ����Ȥ��ˤ�����
���ޤˤ��ξ���
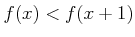 ��Ʊ���ȴ��㤤���Ƥ��������
�������뤬������Ϥ������㤦��
��Ʊ���ȴ��㤤���Ƥ��������
�������뤬������Ϥ������㤦��
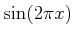 �䡢
�䡢
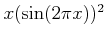 ��ͤ��Ƥߤ���ɤ���(�����̤οޤ⻲��)
��ͤ��Ƥߤ���ɤ���(�����̤οޤ⻲��)
���� 12.2 (``����17�η�'')
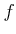
���Ķ��
![$ [a,b]$](img8.png)
��ζ���ñĴ���ä�Ϣ³�ؿ��Ǥ���С�
�εմؿ�
��¸�ߤ��롣
����ˡ�����
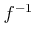
��Ϣ³�ǡ����Ķ���ñĴ���äǤ��롣
�� 12.3
��������
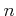
���Ф��ơ�
0
�ʾ�μ¿��������Ȥ���ؿ�
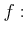
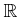
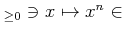
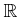
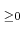
��Ϣ³�Ǥ��ꡢ����ñĴ���äǤ��롣���δؿ������ͤǤ⤢�뤫�顢
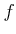
�ϵռ�������ġ����δؿ���
�Ƚ�
�Ĥޤ�
![% latex2html id marker 1015
$ y=\sqrt[n]{x}$](img18.png)
��
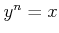
��������ͣ������μ¿��Ǥ��롣
̿�� 12.4
Ǥ�դ����μ¿�
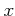
���Ф��ơ�
���ʤꤿ�ġ�
Proof.
![% latex2html id marker 1031
$ y=\sqrt[n]{x}$](img23.png)
�Ȥ����ȡ�����ˤ�ꡢ
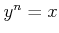
.
�椨�ˡ�
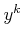
��
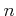
�褷��
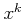
�ˤʤ�¿��Ǥ��롣
���Τ褦�ʼ¿���ͣ��ġ����ʤ��
![% latex2html id marker 1043
$ \sqrt[n]{x^k}$](img27.png)
�����ʤ��ΤǤ��뤫�顢
ξ�Ԥ���������
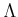
Ʊ�ͤˤ��ơ����Τ��Ȥ�ʬ���롣
̿�� 12.5
��������
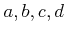
��
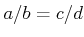
���������С�Ǥ�դμ¿�
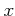
�ˤ������ơ�
���ʤꤿ�ġ�
����̿�꤬�ʤꤿ�ĤΤǡ�
![% latex2html id marker 1058
$ \sqrt[b]{x^a}$](img31.png) �Τ��Ȥ�
�Τ��Ȥ�
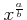 ��
�Ƥ����ζ��줬�ʤ���
��
�Ƥ����ζ��줬�ʤ���
�� 12.6
������Ǥϡ���ǽ������Ѵؿ����μ���
���ΤǤ���Ȥ��롣
-
![$ [-\frac{\pi}{2},\frac{\pi}{2}] \ni x\mapsto \sin(x) \in [-1,1]$](img33.png) �϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
�϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
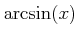 �Ƚ�
�Ƚ�
-
![$ [0,\pi] \ni x\mapsto \cos(x) \in [-1,1]$](img35.png) �϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
�϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
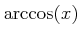 �Ƚ�
�Ƚ�
-
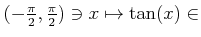
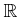 �϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
�϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
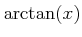 �Ƚ�
�Ƚ�
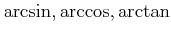 �Ϥ��줾��
�Ϥ��줾��
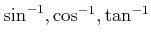 �ʤɤȽ��Ȥ⤢�롣
�ʤɤȽ��Ȥ⤢�롣
���� 12.1
���Τ��Ȥ��ʤ�����
����ͤ������ξ���������ˤʤäƤ��ޤä��Τǡ������Ǥ��ξ�����Ƥ�������
![$ f: [a,b]\to$](img44.png)
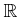 ���Ф��ơ�
���Ф��ơ�
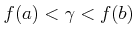 �Ȳ��ꤹ�롣
�Ȳ��ꤹ�롣
![$\displaystyle S=\{c \in [a,b]; \forall x \in [a,c]$](img46.png)
�ˤ�������
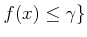
�Ȥ�����
����
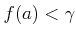 �ˤ��
�ˤ�� 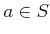 ���狼�롣
�Ȥ��ˡ�
���狼�롣
�Ȥ��ˡ�
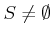 �Ǥ��롣
¾����
�Ǥ��롣
¾���� 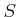 ��
�� ![$ [a,b]$](img8.png) ����ʬ��������顢
ͭ�����椨�ˡ�
����ʬ��������顢
ͭ�����椨�ˡ�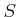 �Ͼ��
�Ͼ�� 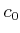 ���ġ�
���ġ�
-
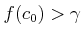 �ξ�硣
�ξ�硣
���� (
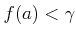 ) �ˤ��
) �ˤ��
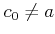 ���狼�롣
���狼�롣
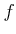 ��
�� 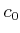 �ˤ�����Ϣ³�Ǥ��뤫�顢
�ˤ�����Ϣ³�Ǥ��뤫�顢
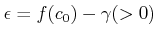 ���Ф��ơ�
����
���Ф��ơ�
���� 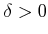 ��¸�ߤ��ơ�
��¸�ߤ��ơ�
![$\displaystyle (x\in [a,b ]$](img57.png)
and
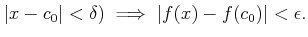
�Ȥ��ˡ�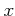 �Ȥ���
�Ȥ���
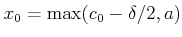 ��Ȥ��,
��Ȥ��,
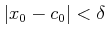 ����
����
![$ x_0\in [a,b]$](img61.png) �Ǥ��뤫�顢
�Ǥ��뤫�顢
|
(12.1) |
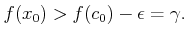 |
¾���� 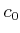 ��
�� 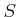 �ξ�¤Ǥ��뤫�顢
�ξ�¤Ǥ��뤫�顢
![$ S \cap (x_0,c_0]$](img63.png) �ˤ�
���븵
�ˤ�
���븵 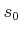 ��¸�ߤ��롣
��¸�ߤ��롣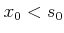 �Ǥ��뤳�Ȥȡ�
�Ǥ��뤳�Ȥȡ�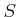 �������
�ߤ�ȡ�
�������
�ߤ�ȡ�
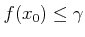 ���狼�롣 ����� (12.1)����̷�⤹�롣
���狼�롣 ����� (12.1)����̷�⤹�롣
-
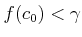 �ξ�硣
�ξ�硣
���� (
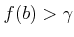 ) �ˤ��
) �ˤ�� 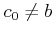 ���狼�롣
���狼�롣
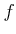 ��
�� 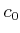 �ˤ�����Ϣ³�Ǥ��뤫�顢
�ˤ�����Ϣ³�Ǥ��뤫�顢
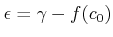 ���Ф��ơ�
����
���Ф��ơ�
���� 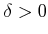 ��¸�ߤ��ơ�
��¸�ߤ��ơ�
![$\displaystyle (x\in [a,b ]$](img57.png)
and
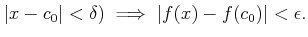
�Ȥ��ˡ�
![$ x\in (c_0-\delta, c_0+\delta)\cap [a,b]$](img71.png) �ʤ�
Ǥ�դ�
�ʤ�
Ǥ�դ� 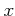 ���Ф��ơ�
���Ф��ơ�
|
(12.2) |
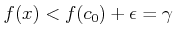 |
¾���� 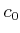 ��
�� 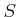 �ξ�¤Ǥ��뤫�顢
�ξ�¤Ǥ��뤫�顢
![$ S \cap (c_0-\delta,c_0]$](img73.png) �ˤ�
���븵
�ˤ�
���븵 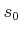 ��¸�ߤ��롣
��¸�ߤ��롣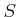 ������ˤ�ꡢ
������ˤ�ꡢ
![$\displaystyle \forall x \in [a,s_0]$](img74.png)
������
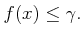
���Τ��Ȥ� (12.2)����ʻ����ȡ�
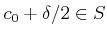 ���������졢
�����
���������졢
����� 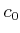 �������̷�⤹�롣
�������̷�⤹�롣
�ʾ�ˤ�ꡢ
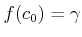 .
.
���ͤޤǤ���� 12.1 �β������դǽҤ٤�
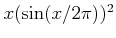 �Υ���դ�
�ܤ��Ƥ�������
�Υ���դ�
�ܤ��Ƥ�������
![\includegraphics[scale=0.5]{12-01.eps}](img79.png)



Next: About this document ...
2011-07-01
![]()
![]() ��Ʊ���ȴ��㤤���Ƥ��������
�������뤬������Ϥ������㤦��
��Ʊ���ȴ��㤤���Ƥ��������
�������뤬������Ϥ������㤦��
![]() �䡢
�䡢
![]() ��ͤ��Ƥߤ���ɤ���(�����̤οޤ⻲��)
��ͤ��Ƥߤ���ɤ���(�����̤οޤ⻲��)
![]()
![]() ���Ф��ơ�
���Ф��ơ�
![]() �Ȳ��ꤹ�롣
�Ȳ��ꤹ�롣
![]() ) �ˤ��
) �ˤ��
![]() ���狼�롣
���狼�롣
![]() ��
�� ![]() �ˤ�����Ϣ³�Ǥ��뤫�顢
�ˤ�����Ϣ³�Ǥ��뤫�顢
![]() ���Ф��ơ�
����
���Ф��ơ�
���� ![]() ��¸�ߤ��ơ�
��¸�ߤ��ơ�
![]() ) �ˤ��
) �ˤ�� ![]() ���狼�롣
���狼�롣
![]() ��
�� ![]() �ˤ�����Ϣ³�Ǥ��뤫�顢
�ˤ�����Ϣ³�Ǥ��뤫�顢
![]() ���Ф��ơ�
����
���Ф��ơ�
���� ![]() ��¸�ߤ��ơ�
��¸�ߤ��ơ�
![]() .
.
![]() �Υ���դ�
�ܤ��Ƥ�������
�Υ���դ�
�ܤ��Ƥ�������
![\includegraphics[scale=0.5]{12-01.eps}](img79.png)