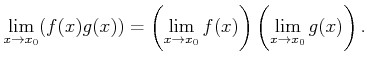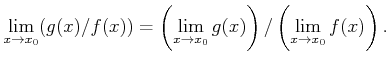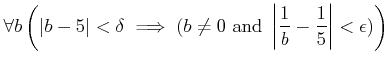๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 9.1 (๏ฟฝฦท๏ฟฝ)
[``๏ฟฝ๏ฟฝ๏ฟฝสฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 10'']
๏ฟฝหธ๏ฟฝ
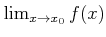
๏ฟฝ๏ฟฝ
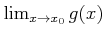
๏ฟฝ๏ฟฝ๏ฟฝศค๏ฟฝ๏ฟฝ
ยธ๏ฟฝ฿ค๏ฟฝ๏ฟฝ๏ฟฝศฒ๏ฟฝ๏ฟฝ๊คน๏ฟฝ๋กฃ๏ฟฝ๏ฟฝ๏ฟฝฮคศค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮค๏ฟฝ๏ฟฝศค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฉ๏ฟฝฤก๏ฟฝ
-
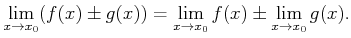
-
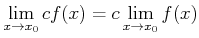 .
.
-
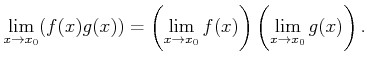
- ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝหก๏ฟฝ
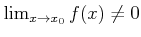 ๏ฟฝศฒ๏ฟฝ๏ฟฝ๊คน๏ฟฝ๏ฟฝศก๏ฟฝ
๏ฟฝศฒ๏ฟฝ๏ฟฝ๊คน๏ฟฝ๏ฟฝศก๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 9.1
๏ฟฝ๏ฟฝ๏ฟฝฮฟ๏ฟฝ
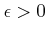
๏ฟฝ๏ฟฝอฟ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฦค๏ฟฝ๏ฟฝ๏ฟฝศค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝ๏ฟฝ๏ฟฝฮคศค๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝฮค่คฆ๏ฟฝ๏ฟฝ ๏ฟฝ๏ฟฝ๏ฟฝฮฟ๏ฟฝ
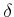
๏ฟฝ๒ธซคฤค๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
![]()