


Next: About this document ...
��ʬ��ʬ�س���AI���� No.2
��2���ܤμ��� :

���θ����ϼ¿��δ���Ū�������Ǥ��롣
���� 2.1
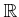
����ʬ����
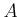
�����ͭ���ʤ�С�
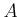
�Ͼ�¤���ġ�
��� 2.2
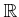
����ʬ����
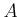
���Ф��ơ����ξ�¤Τ��Ȥ�
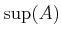
�Ƚ�
���� 2.3
����
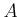
���
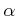
�Ǥ��뤳�Ȥϡ��������郎Ʊ��������Ω�Ĥ��Ȥ�
Ʊ�ͤǤ��롣
-
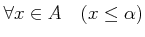 .
.
-
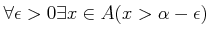 .
.
��
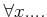 ��
�ϡ��֤ɤ��
��
�ϡ��֤ɤ�� 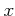 ���Ф��Ƥ⡢
���Ф��Ƥ⡢ 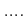 ���ʤꤿ�ġפȤ�����̣��
���ʤꤿ�ġפȤ�����̣��
��
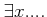 ��
�ϡ��֤ʤˤ������Ĥ�
��
�ϡ��֤ʤˤ������Ĥ� 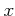 ���Ф��Ƥϡ�
���Ф��Ƥϡ� 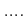 ���ʤꤿ�ġפȤ�����̣���Ѥ��롣
���ʤꤿ�ġפȤ�����̣���Ѥ��롣
�������������ΤΤ��Ȥιֵ��Ǥ�
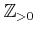 �Ƚ�
����Ȥϡ�����Ū�ˤϼ��Τ褦������Ǥ��롣
�Ƚ�
����Ȥϡ�����Ū�ˤϼ��Τ褦������Ǥ��롣
��� 2.4
�¿���
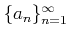
�Ȥϡ�
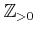
����
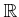
�ؤμ���
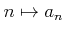
(���ʤ������������
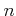
�˼¿�
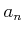
���б��������б�)�Τ��ȤǤ��롣
���� 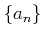 ��ñ�ʤ뽸��ȸ��Ƥ��줬ͭ�����ɤ�������
����
��ñ�ʤ뽸��ȸ��Ƥ��줬ͭ�����ɤ�������
���ξ�� 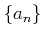 ��������뤳�Ȥ��Ǥ��롣���� 2.1�ˤ�ꡢ
���ͭ���ʿ����
��¤���Ĥ��Ȥ��狼�롣
��������뤳�Ȥ��Ǥ��롣���� 2.1�ˤ�ꡢ
���ͭ���ʿ����
��¤���Ĥ��Ȥ��狼�롣
��� 2.5
�¿���
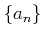
��
ñĴ�����Ǥ���Ȥϡ�
���ʤꤿ�ĤȤ��ˤ�����
��ä�Ϫ���˸����� 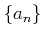 ��ñĴ���äǤ���Ȥ�
��ñĴ���äǤ���Ȥ�
������Ω�ĤȤ������ȤǤ��롣
���� 2.6
����
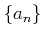
��
��������롣���ΤȤ�
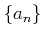 ��ñĴ���äǤ��롣
��ñĴ���äǤ��롣
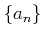 ��ͭ���Ǥ��롣
��ͭ���Ǥ��롣
��� 2.7
���
�Τ��Ȥ�
�����п������Ȥ�ӡ�
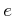
�Ƚ�
���� 2.1
���μ¿�
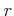
��ҤȤĸ��ꤷ���Ȥ���
�������������
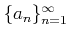
�Ͼ��ͭ���Ǥ��뤳�Ȥ��ʤ�����
���ͤΤ���ˡ�
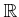 ��������ɬ�Ǿ��¤Τ�Τ�Ƥ�������
��������ɬ�Ǿ��¤Τ�Τ�Ƥ�������
�褯�ΤäƤ�����
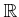 ���龯��Υ��ơ����Τ褦�ʽ���
���龯��Υ��ơ����Τ褦�ʽ��� 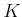 (�Ȥ��ξ�α黻
(�Ȥ��ξ�α黻 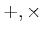 ,��
,�� 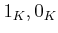 ,�ط���
,�ط��� 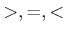 )��ͤ��롣
)��ͤ��롣
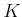 ���ΤǤ��롣���ʤ��:
���ΤǤ��롣���ʤ��:
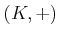 �ϲ�ˡ���Ǥ��롣
�ϲ�ˡ���Ǥ��롣
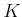 �γƸ�
�γƸ� 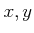 ���Ф��ơ������¤ȸƤФ�븵
���Ф��ơ������¤ȸƤФ�븵 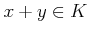 ��
�����ҤȤ���ޤ롣
��
�����ҤȤ���ޤ롣
-
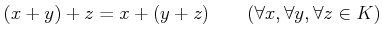 .
.
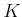 �ˤϥ�����
�ˤϥ����� 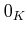 �ȸƤФ�븵��¸�ߤ��ơ�
Ǥ�դ�
�ȸƤФ�븵��¸�ߤ��ơ�
Ǥ�դ� 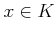 ���Ф���
������
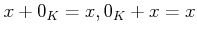 ����������
����������
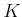 �γƸ�
�γƸ� 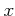 ���Ф��ơ����Υޥ��ʥ���
���Ф��ơ����Υޥ��ʥ��� 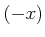 �ȸƤФ�븵��
¸�ߤ��ơ�
�ȸƤФ�븵��
¸�ߤ��ơ�
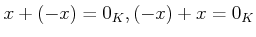 ����������
����������
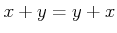 .
.
-
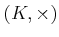 �Ͼ�ˡ�˴ؤ���Ⱦ����ʤ������ʤ����
�Ͼ�ˡ�˴ؤ���Ⱦ����ʤ������ʤ����
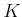 �γƸ�
�γƸ� 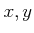 ���Ф��ơ������ѤȸƤФ�븵
���Ф��ơ������ѤȸƤФ�븵 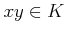 ��
�����ҤȤ���ޤ롣
��
�����ҤȤ���ޤ롣
-
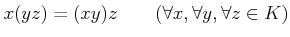 .
.
- ʬ��ˡ§��
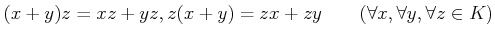 .
.
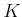 �Ͼ�ˡ�˴ؤ���ñ�̸�
�Ͼ�ˡ�˴ؤ���ñ�̸� 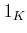 ���ġ����ʤ����
Ǥ�դ�
���ġ����ʤ����
Ǥ�դ� 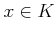 ���Ф���
������
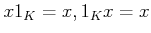 ����������
����������
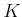 �ξ�ˡ�ϲĴ��Ǥ��롣
�ξ�ˡ�ϲĴ��Ǥ��롣
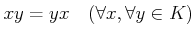 .
.
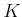 ��
�� 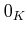 �ʳ��θ�
�ʳ��θ� 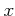 �Ͼ�ˡ�˴ؤ��Ƶո�
�Ͼ�ˡ�˴ؤ��Ƶո� 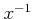 �ȸƤФ�븵��¸�ߤ��ơ�
�ȸƤФ�븵��¸�ߤ��ơ�
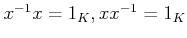 ����������
����������
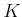 �����������Ǥ��롣
�����������Ǥ��롣
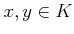 ���Ф��ơ�
���Ф��ơ� 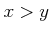 ��
�� 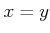 ��
�� 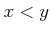 �Τ����줫������Ω�ġ�
�Τ����줫������Ω�ġ�
-
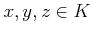 �ˤ������ơ���(
�ˤ������ơ���(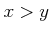 and
and 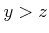 ) �ʤ��
) �ʤ�� 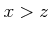 �פ�����Ω�ġ�
�פ�����Ω�ġ�
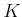 ���Τι�¤�Ƚ����¤��ξΩ���롣
���Τι�¤�Ƚ����¤��ξΩ���롣
-
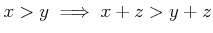 .
.
-
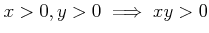 .
.
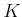 ��Ǥ�դ�ͭ����ʬ�����
��Ǥ�դ�ͭ����ʬ����� 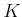 ��˾�¤���ġ�
��˾�¤���ġ�
���ΤȤ���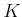 �ϼ¿���
�ϼ¿���
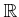 �ȡ�Ʊ����(����ΤȤ���Ʊ��)�Ǥ��롣
�ȡ�Ʊ����(����ΤȤ���Ʊ��)�Ǥ��롣
������ˡ�����ΤˤĤ��ơ����ξܤ���������2ǯ�����������ؤǿ����ٶ����롣



Next: About this document ...
2011-04-15
![]()
![]() ��
�ϡ��֤ɤ��
��
�ϡ��֤ɤ�� ![]() ���Ф��Ƥ⡢
���Ф��Ƥ⡢ ![]() ���ʤꤿ�ġפȤ�����̣��
���ʤꤿ�ġפȤ�����̣��
![]() ��
�ϡ��֤ʤˤ������Ĥ�
��
�ϡ��֤ʤˤ������Ĥ� ![]() ���Ф��Ƥϡ�
���Ф��Ƥϡ� ![]() ���ʤꤿ�ġפȤ�����̣���Ѥ��롣
���ʤꤿ�ġפȤ�����̣���Ѥ��롣
![]() �Ƚ�
����Ȥϡ�����Ū�ˤϼ��Τ褦������Ǥ��롣
�Ƚ�
����Ȥϡ�����Ū�ˤϼ��Τ褦������Ǥ��롣
![]() ��ñ�ʤ뽸��ȸ��Ƥ��줬ͭ�����ɤ�������
����
��ñ�ʤ뽸��ȸ��Ƥ��줬ͭ�����ɤ�������
���ξ�� ![]() ��������뤳�Ȥ��Ǥ��롣���� 2.1�ˤ�ꡢ
���ͭ���ʿ����
��¤���Ĥ��Ȥ��狼�롣
��������뤳�Ȥ��Ǥ��롣���� 2.1�ˤ�ꡢ
���ͭ���ʿ����
��¤���Ĥ��Ȥ��狼�롣
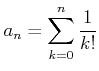
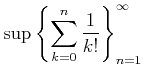
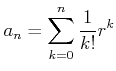
![]() ��������ɬ�Ǿ��¤Τ�Τ�Ƥ�������
��������ɬ�Ǿ��¤Τ�Τ�Ƥ�������
![]() ���龯��Υ��ơ����Τ褦�ʽ���
���龯��Υ��ơ����Τ褦�ʽ��� ![]() (�Ȥ��ξ�α黻
(�Ȥ��ξ�α黻 ![]() ,��
,�� ![]() ,�ط���
,�ط��� ![]() )��ͤ��롣
)��ͤ��롣
![]() �ϼ¿���
�ϼ¿���
![]() �ȡ�Ʊ����(����ΤȤ���Ʊ��)�Ǥ��롣
�ȡ�Ʊ����(����ΤȤ���Ʊ��)�Ǥ��롣