Commutative algebra

Yoshifumi Tsuchimoto

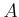
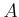
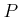
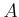
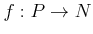
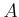
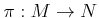
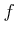
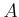
DEFINITION 09.1   Let $A$ be a ring. an $A$ -module $P$ is said to be projective if it satisfies the following condition: For any $A$ -module morphism $f: P \to N$ and for any surjective $A$ -module homomorphism $\pi:M \to N$ , $f$ ``lifts'' to an $A$ -module morphism $\hat f: M\to I$ .

$$\begin{CD} P @>\hat f >>M \\ @\vert @V\pi VV \\ P @>f >> N \end{CD}$$

LEMMA 09.2   An $A$ -module $M$ is projective if and only if it is a direct summand of a free $A$ -module.

PROPOSITION 09.3   Let $B$ be a 0 -smooth algebra over a ring $A$ . Then $\Omega^1_{B/A}$ is projective.

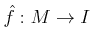
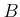
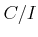
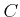
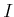
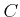
PROOF.. Let us express the algebra $B$ as a quotient $C/I$ where $C$ is a polynomial algebra and $I$ is an ideal of $C$ . Then by Theorem 08.5, we know that

$$0\to I/I^2 \to \Omega^1_{C}\otimes_C B \to \Omega^1_B \to 0$$

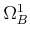
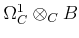
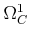
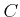
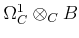
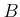
is split exact. So $\Omega^1_B$ is a direct sum of $\Omega^1_{C}\otimes_C B$ . On the other hand, $\Omega^1_{C}$ is free $C$ -module so that $\Omega^1_{C}\otimes_C B$ is also a free $B$ -module.

$\qedsymbol$

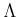
We would like to define ``smoothness'' as a something good. Especially, we would expect ``smooth algebras'' to be flat. But that is not always true if we regard ``smoothness'' as 0 -smoothness. The following example is an easy case of [1, example 7.2].

EXAMPLE 09.4   Let us put $A=\mathbb{C}[\{\sqrt[2^n]{T}\}_{n=1}^\infty ] =\mathbb{C}[T,\sqrt{T},\sqrt[2]{T},\sqrt[4]{T},\dots,]$ and put

$$I=\{f \in A; f(0)=0\}=\sum_{n=1}^\infty \sqrt[2^n]{T} A.$$

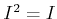
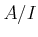
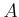
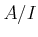
Then we see that $I^2=I$ . Thus $A/I$ is 0 -smooth over $A$ . where as $A/I$ is not flat over $A$ .

DEFINITION 09.5   Let $A$ be a ring.

1. An $A$ -algebra $B$ is said to be finitely generated over $A$ if $B$ is generated by a finite set as an $A$ -algebra. In other words, it is finitely generated if there exists a surjective $A$ -algebra homomorphism from a finitely generated polynomial ring $A[X_1,X_2,\dots,X_r]$ to $B$ .
2. An $A$ -algebra $B$ is said to be finitely presented over $A$ if there exists a surjective $A$ -algebra homomorphism $\varphi$ from a finitely generated polynomial ring $P=A[X_1,X_2,\dots,X_r]$ to $B$ such that its kernel is a finitely generated ideal of $P$ . is a finitely generated ideal of $P$ .

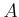
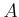
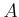
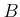
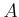
DEFINITION 09.6   Let $A$ be a ring. An $A$ -algebra $B$ is said to be smooth over $A$ if it is 0 -smooth and finitely presented over $A$ .

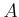
We may define unramified/étale algebras in a same manner.

Let us recall the definition of Noetherian ring.

DEFINITION 09.7   A ring is called Noetherian if its ideals are always finitely generated.

PROPOSITION 09.8  

If $A$ is Noetherian, then:

1. Any of its quotient ring is Noetherian.
2. The polynomial ring $A[X]$ is Noetherian.

It follows that any finitely generated $A$ -algebra $B$ is also Noetherian. We note also that $B$ is finitely presented over $A$ in this case.