


Next: Bibliography
Commutative algebra
Yoshifumi Tsuchimoto
DEFINITION 09.1
Let
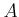
be a ring. an
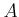
-module
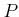
is said to be
projective if it satisfies the following condition:
For any
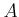
-module morphism
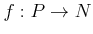
and
for any surjective
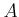
-module homomorphism
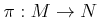
,
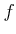
``lifts'' to an
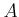
-module morphism
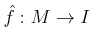
.
PROOF..
Let us express the algebra
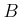
as a quotient
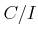
where
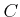
is a polynomial algebra and
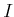
is an ideal of
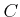
. Then by Theorem 08.5, we know that
is split exact.
So
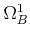
is a direct sum of
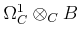
.
On the other hand,
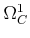
is free
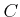
-module so
that
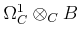
is also a free
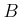
-module.
We would like to define ``smoothness'' as a something good. Especially,
we would expect ``smooth algebras'' to be flat. But that is not always true
if we regard ``smoothness'' as 0
-smoothness.
The following example is an easy case of [1, example 7.2].
EXAMPLE 09.4
Let us put
![% latex2html id marker 824
$ A=\mathbb{C}[\{\sqrt[2^n]{T}\}_{n=1}^\infty ]
=\mathbb{C}[T,\sqrt{T},\sqrt[2]{T},\sqrt[4]{T},\dots,]$](img20.png)
and put
Then we see that
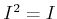
. Thus
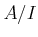
is 0
-smooth over
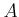
.
where as
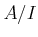
is not flat over
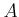
.
DEFINITION 09.6
Let
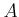
be a ring.
An
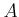
-algebra
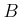
is said to be
smooth over
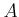
if it is 0
-smooth and finitely
presented over
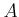
.
We may define unramified/étale algebras in a same manner.
Let us recall the definition of Noetherian ring.
DEFINITION 09.7
A ring is called
Noetherian if its ideals are always finitely generated.



Next: Bibliography
2011-07-21
![]()
![]()
![% latex2html id marker 826
$\displaystyle I=\{f \in A; f(0)=0\}=\sum_{n=1}^\infty \sqrt[2^n]{T} A.
$](img21.png)
![]() is Noetherian, then:
is Noetherian, then: