


Next: local rings
Commutative algebra
Yoshifumi Tsuchimoto

DEFINITION 02.1
Let
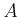
be a commutative ring. Let
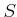
be its subset.
We say that
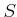
is multiplicative if
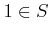
-
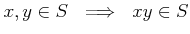
holds.
DEFINITION 02.2
Let
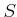
be a multiplicative subset of a commutative ring
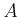
.
Then we define
![$ A[S^{-1}]$](img6.png)
as
where in the above notation
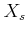
is a indeterminate prepared for each element
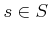
.)
We denote by
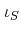
a canonical map
![$ A\to A[S^{-1}]$](img11.png)
.
There is another description of ![$ A[S^{-1}]$](img6.png) . Namely, We consider an
equivalence relateion
. Namely, We consider an
equivalence relateion 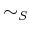 on a set
on a set
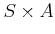 by
by
We call the quotient space space
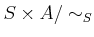 as
as 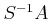 .
The equivalence class of
.
The equivalence class of
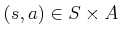 in
in 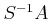 is denoted
by
is denoted
by 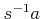 .
Then it is easy to introduce a ring structure of
.
Then it is easy to introduce a ring structure of 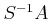 and see that
and see that
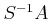 actually satisfies the universal property of
actually satisfies the universal property of ![$ A[S^{-1}]$](img6.png) .
We thus have a canonical isomorphism
.
We thus have a canonical isomorphism
![$ S^{-1}A\cong A[S^{-1}]$](img33.png) .
.
EXAMPLE 02.5
![$ A_f=A[S^{-1}]$](img34.png)
for
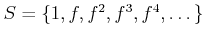
.
The total ring of quotients
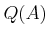
is defined as
![$ A[S^{-1}]$](img6.png)
for
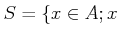
is not a zero divisor of A
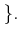
When
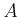
is an integral domain, then
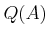
is the field of quotients of
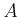
.
DEFINITION 02.6
Let
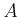
be a commutative ring. Let
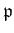
be its prime ideal. Then we define
the localization of
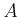
with respect to
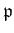
by
DEFINITION 02.7
Let
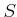
be a multiplicative subset of a commutative ring
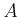
.
Let
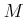
be an
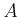
-module
we may define
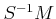
as
where the equivalence relation
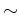
is defined by
We may introduce a
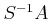
-module structure on
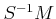
in
an obvious manner.
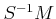 thus constructed satisfies an universality condition which
the reader may easily guess.
thus constructed satisfies an universality condition which
the reader may easily guess.
By a universality argument, we may easily see the following proposition.
PROPOSITION 02.9
Let 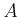 be a commutative ring. Let
be a commutative ring. Let 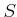 be a multiplicative subet of
be a multiplicative subet of 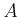 .
Then the natural homomorphism
.
Then the natural homomorphism
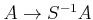 is flat.
is flat.



Next: local rings
2011-04-21
![]() be a ring,
be a ring,
![]() be a ring homomorphism such that
be a ring homomorphism such that
![]() is invertible in
is invertible in ![]() for any
for any ![]() .
Then there exists a unique ring homomorphism
.
Then there exists a unique ring homomorphism
![]() such that
such that
![]() thus constructed satisfies an universality condition which
the reader may easily guess.
thus constructed satisfies an universality condition which
the reader may easily guess.