

![]()
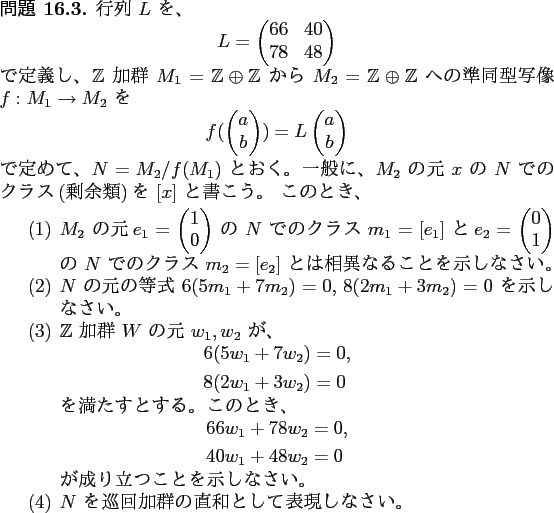
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―

![]()
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ― ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŽïŋ―ŅĪïŋ―ïŋ―ïŋ―ÐĪïĪŦïŋ―ëĄĢ
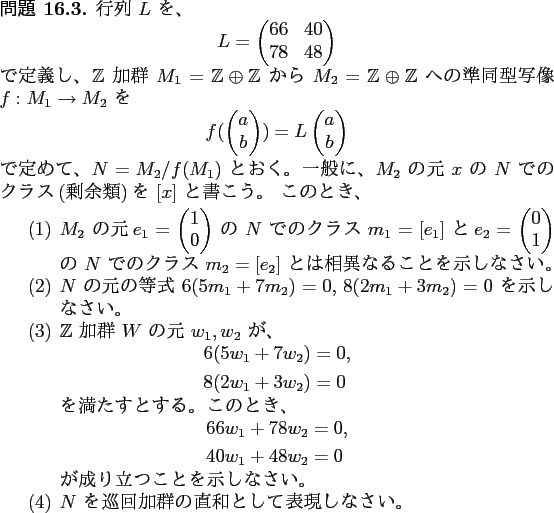
(1)
![]() ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ČĄïŋ―
![]() ïŋ―ČĪĘĪëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪĘĪëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ÆĄïŋ―
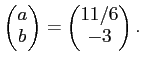
ïŋ―ïŋ―(16.1)ïŋ―ïŋ―ÍĢïŋ―ïŋ―Îēïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ïĪŦïŋ―ëĄĢïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―(16.1) ïŋ―ïŋ― ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(2)
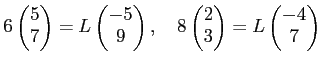
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―Ø·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĪŦïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
(3) ïŋ―Ęēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ÎŽïŋ―ïŋ―ËĄïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―čĪĶïŋ―ïŋ―ïŋ―ïĪŦïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ― ÅŽïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ČĪË―ņĪĪĪÆĪßĪïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―
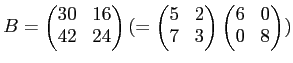
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
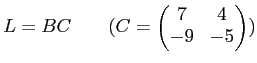
ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ
(4)
![]() ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ― ![]() ,
, ![]() ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―Îīïŋ―ïŋ―ÜīØ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ÎŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―Îīïŋ―ïŋ―ÜīØ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ÎŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ ïŋ―ïŋ―ïŋ―ÎīØ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ãąïŋ―ËĪïŋ―ïŋ―čĪĶïŋ―ïŋ― (2),(3) ïŋ―ËĪïŋ―ęĄĒ(ïŋ―ïŋ―ïŋ―ëĪĪïŋ―ÏĄïŋ―
ïŋ―ïŋ―Æąïŋ―ÍĪĮĪïŋ―ïŋ―ëĄĢ Âūïŋ―ïŋ―
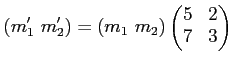
ïŋ―Ïīïŋ―ïŋ―ïŋ―ïŋ―Ņīïŋ―ïŋ―ΰïŋ―ÄĪĮĪïŋ―ïŋ―ęĄĒïŋ―åĩïŋ―Ø·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ïĪŦïŋ―ëĄĢ ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
[ïŋ―ïŋ―ïŋ―ïŋ―ÎĨïŋ―ïŋ―ïŋ―ïŋ―ËĪĘĪïŋ―ÎĪÏĄïŋ―(2)ïŋ―Îēïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌĪČĪÄĪËĪÞĪČĪáĪŋ
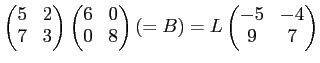
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ÐūėĪđïŋ―ïŋ―
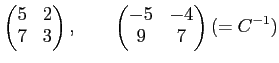
ïŋ―ïŋ―ïŋ―ïŋ―ÄĪÎđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĩÕđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ĮĪïŋ―ïŋ―ëĄĢ ]