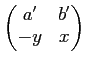Next: About this document ...
�����II���� No.7
��7���ܤμ��� :

��� 7.1
��
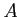
��β÷�
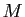
�θ�
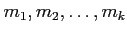
���Ф��ơ�
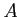
-��Ʊ��
�γ�
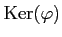
�θ��Τ��Ȥ�
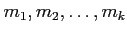
��
�ط����ȸƤӡ�
�������ΤΤʤ��÷�
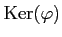
�Τ��Ȥ�
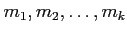
��
�ط����Τʤ��÷��ȸƤ֡�
�ʲ��Ǥϡ����Τ褦���Ѵ���ͤ��롣
- �Ѵ�1.
-
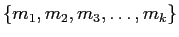 �ν�������촹���롣
�ν�������촹���롣
- �Ѵ�2.
-
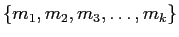 �������
�����
�������
�����
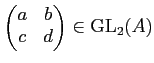 �ǡ֤Ҥͤä���
�ǡ֤Ҥͤä���
��ͤ��롣
- �Ѵ�3.
-
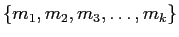 �������
������� 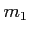 ��
��
���֤����������
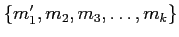 ��ͤ��롣
��ͤ��롣
(�Ѵ�3)��(�Ѵ�1), (�Ѵ�2)��Í�²��Ȥ߹�碌�������뤳�Ȥ�
�狼��Τ�
�ʲ��ε�����ɬ�ܤǤϤʤ���
���� 7.2 (�Ѵ�1)
,(�Ѵ�2),(�Ѵ�3)�η����Ѵ���(Ʊ������)���Ѵ����ġ�
�Ȥ��ˡ�
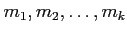
��
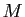
����������ʤ�С������
(�Ѵ�1),(�Ѵ�2),(�Ѵ�3) ��Í�²󷫤��֤�������줿�Ȥ߹�碌
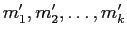
��
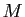
���������롣
�������Τ褦�� 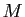 ��
��
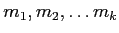 ��Ϳ����줿�Ȥ���
��Ϳ����줿�Ȥ���
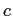 ���������Τθ�����դ���
�⤷���줬����ʪ�פǤϤʤ����ˤϾ����ˤ���褦�������Ѥ���
���������Ѵ����༡�Ԥ����Ȥˤ�ꡢ
���������Τθ�����դ���
�⤷���줬����ʪ�פǤϤʤ����ˤϾ����ˤ���褦�������Ѥ���
���������Ѵ����༡�Ԥ����Ȥˤ�ꡢ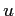 ����륢�르�ꥺ���
�������뤳�Ȥ��Ǥ��롣Ʊ�ͤˤ��Ƽ���������
����륢�르�ꥺ���
�������뤳�Ȥ��Ǥ��롣Ʊ�ͤˤ��Ƽ��������� 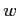 �����륢�르�ꥺ���
�����롣
�����륢�르�ꥺ���
�����롣
���� 7.4
�Ĵ� PID
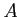
���Í�������÷�
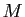
��Ϳ�����Ƥ���Ȥ��롣
���ΤȤ���
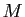
��������
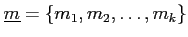
�ˤ������ơ�
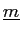
��(�Ѵ�1),(�Ѵ�2),(�Ѵ�3)��Í�²󷫤��֤����Ȥˤ�ꡢ
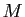
�����������
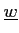
�Ǥ��äơ�
�Ȥʤ��Τ�¸�ߤ��롣
��� 7.5
��Ĥθ������������÷������÷��ȸƤ֡�
̿�� 7.7 (�����θ�������)
�Ĵ� PID
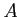
���Ǥ�դ�Í�������÷�
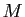
�Ͻ��
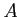
�÷���ľ�¤�Ʊ���Ǥ��롣
�椨�ˡ�����
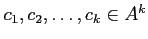
��
�ʤ�Ʊ����¸�ߤ��롣
(������)�÷���
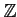 -�÷��Τ��Ȥ�Ʊ���Ǥ��äơ�
-�÷��Τ��Ȥ�Ʊ���Ǥ��äơ�
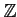 ��
�� 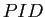 �Ǥ��뤳�Ȥ��顢
�Ĥ���(����Í�Ѥ��Ľ��פ�)�Ϥ�����Ω�ġ�
�Ǥ��뤳�Ȥ��顢
�Ĥ���(����Í�Ѥ��Ľ��פ�)�Ϥ�����Ω�ġ�
�� 7.8 (Í�����������٥뷲�δ�������)
Ǥ�դ�Í�����������٥뷲�Ͻ�󷲤�Í�¸Ĥ�ľ�¤Ǥ��롣
���� 7.1
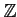
-�÷�
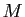
��2�Ĥθ�
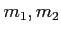
����������Ƥ��ơ����δط������������Ȥ��롣
����ʳ������ʤδط������ʤ��Ȥ���Ȥ���
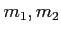
��(�Ѵ�1),(�Ѵ�2),(�Ѵ�3)
��Í�²�ܤ����Ȥˤ�ꡢ������������
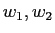
�����ơ�
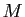
����÷���ľ�¤Ȥ���ɽ�����衣
����:
̿�� 7.9
�Ĵ� PID
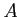
�θ�
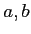
���Ф��ơ����ǥ���
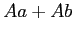
��
����ñ�।�ǥ���
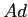
�������������ΤȤ�������
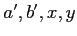
��¸�ߤ��ơ�
�����󼰤�����Ω�ġ�
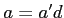 ,
, 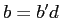 .
.
-
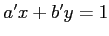 .
.
�Ȥ��ˡ�
��
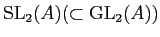
�θ��Ǥ��롣
̿�� 7.10
�Ĵ� PID
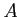
�Υ��ǥ����������
��ɬ��Í�¤ǻߤޤ롣���ʤ��������
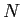
�����äơ�
������Ω�ġ�



Next: About this document ...
2010-06-01
![]()
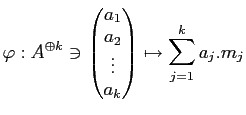
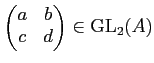 �ǡ֤Ҥͤä���
�ǡ֤Ҥͤä���
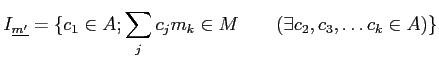
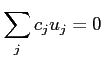
![]() ��
��
![]() ��Ϳ����줿�Ȥ���
��Ϳ����줿�Ȥ���
![]() ���������Τθ�����դ���
�⤷���줬����ʪ�פǤϤʤ����ˤϾ����ˤ���褦�������Ѥ���
���������Ѵ����༡�Ԥ����Ȥˤ�ꡢ
���������Τθ�����դ���
�⤷���줬����ʪ�פǤϤʤ����ˤϾ����ˤ���褦�������Ѥ���
���������Ѵ����༡�Ԥ����Ȥˤ�ꡢ![]() ����륢�르�ꥺ���
�������뤳�Ȥ��Ǥ��롣Ʊ�ͤˤ��Ƽ���������
����륢�르�ꥺ���
�������뤳�Ȥ��Ǥ��롣Ʊ�ͤˤ��Ƽ��������� ![]() �����륢�르�ꥺ���
�����롣
�����륢�르�ꥺ���
�����롣
![]() -�÷��Τ��Ȥ�Ʊ���Ǥ��äơ�
-�÷��Τ��Ȥ�Ʊ���Ǥ��äơ�
![]() ��
�� ![]() �Ǥ��뤳�Ȥ��顢
�Ĥ���(����Í�Ѥ��Ľ��פ�)�Ϥ�����Ω�ġ�
�Ǥ��뤳�Ȥ��顢
�Ĥ���(����Í�Ѥ��Ľ��פ�)�Ϥ�����Ω�ġ�