


Next: About this document ...
�����II���� No.5
��5���ܤμ��� :

��� 5.1
��
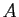
��β÷�
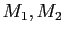
��Ϳ�����Ƥ���Ȥ��롣
ľ�ѽ���
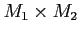
�˼��Τ褦���¡������顼�ܤ��������
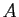
-�÷��ι�¤������뤳�Ȥ��Ǥ��롣
���β÷���
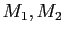
��
ľ�� �Ȥ�ӡ�
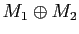
�Ƚ�
ͭ�¸Ĥ� 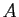 -�÷�
-�÷�
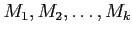 ��ľ��
��ľ��
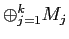 ��
Ʊ�ͤ��������롣
Ʊ���÷�
��
Ʊ�ͤ��������롣
Ʊ���÷�  ��
��  �Ĥ�ľ��
�Ĥ�ľ��
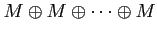 �Τ��Ȥ�
�Τ��Ȥ�
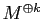 �Ƚ�
�Ƚ�
ľ�¤δ֤μ����ϼ��Τ褦�˹���Ū��ʬ��Ǥ��롣
̿�� 5.3
��
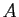
��β÷�
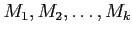
����
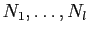
�ؤ�
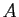
-��Ʊ��
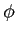
��Ϳ����줿�Ȥ��롣���ΤȤ�
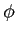
��
��ʬ��롣������
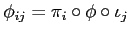
. �����
�ޤ����Τ褦��
ά������롣
��� 5.4
��
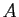
�ˤ�������
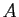
���Ȥ�
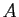
-�÷��Ȥߤʤ����Ȥ��Ǥ��롣
���Τ����Ĥ���ľ�¤Ȥ���������÷�(��
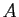
-�÷��Ȥ���Ʊ���ʲ÷�)��
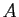
���
��ͳ 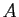 -�÷�
-�÷��ȸƤ֡�
���� 5.5
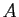
-�÷�
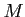
�θ�
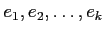
������������������Ȥ��롣
- BASE1.
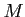 ��
�� 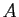 ��
��
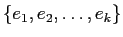 ����������롣���ʤ����
����������롣���ʤ����
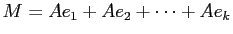 ������Ω�ġ�
������Ω�ġ�
- BASE2.
-
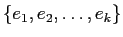 ��
�� 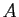 ��켡��Ω�Ǥ��롣
��켡��Ω�Ǥ��롣
���ΤȤ���
��Ʊ���Ǥ���
1��
�Ȥ��ˡ�
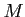
�ϼ�ͳ�÷��Ǥ��롣(���Τ褦�ʾ����λ���
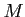
��
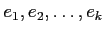 �����Ȥ��뼫ͳ�÷�
�����Ȥ��뼫ͳ�÷��Ǥ���ȸ�����)
�� 5.7
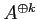
����
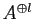
�ؤ�Ǥ�դ�
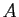
-��Ʊ��
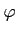
�ϡ�
�Ƚ롣
��� 5.8
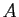
-�÷�
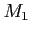
����
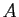
-�÷�
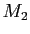
�ؤ�
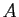
-��Ʊ�������Τ�
�Ƚ�ɽ����
(����������Τ褦��) 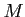 ��
��  -�÷��ʳ��ι�¤��������ˤϡ�
���̤Τ����ΰ�̣��
-�÷��ʳ��ι�¤��������ˤϡ�
���̤Τ����ΰ�̣��
 �Τ��Ȥ�
�Τ��Ȥ�
 ���Ƚ��Ȥ����롣
���Ƚ��Ȥ����롣
���� 5.1
�ϡִĤ�ȿ��Ʊ���פǤ��뤳�ȡ����ʤ����
���ʤ�����



Next: About this document ...
2010-06-16
![]()
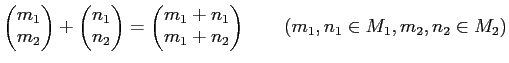
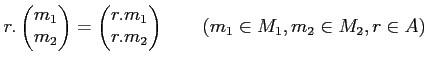
![]() -�÷�
-�÷�
![]() ��ľ��
��ľ��
![]() ��
Ʊ�ͤ��������롣
Ʊ���÷�
��
Ʊ�ͤ��������롣
Ʊ���÷� ![]() ��
�� ![]() �Ĥ�ľ��
�Ĥ�ľ��
![]() �Τ��Ȥ�
�Τ��Ȥ�
![]() �Ƚ�
�Ƚ�
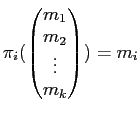
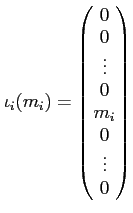 ($i$ ���ܤ���ʬ�Τ� $m_i$ �Ǥ��Ȥ� $0$.)
($i$ ���ܤ���ʬ�Τ� $m_i$ �Ǥ��Ȥ� $0$.)
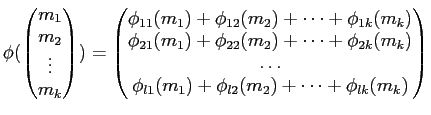
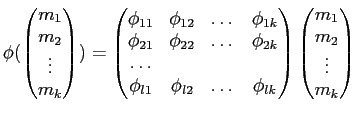
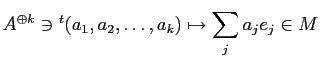
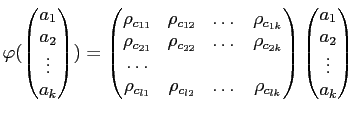
![]() ��
�� ![]() -�÷��ʳ��ι�¤��������ˤϡ�
���̤Τ����ΰ�̣��
-�÷��ʳ��ι�¤��������ˤϡ�
���̤Τ����ΰ�̣��
![]() �Τ��Ȥ�
�Τ��Ȥ�
![]() ���Ƚ��Ȥ����롣
���Ƚ��Ȥ����롣