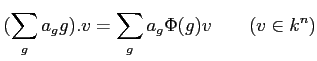Next: About this document ...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―IIïŋ―ïŋ―ïŋ―ïŋ― No.3
ïŋ―ïŋ―3ïŋ―ïŋ―ïŋ―ÜĪΞïŋ―ïŋ―ïŋ― :
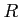 -ïŋ―÷ïŋ―
-ïŋ―÷ïŋ― 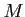 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―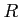 ïŋ―Îļïŋ―ïŋ―ïŋ―
ïŋ―Îļïŋ―ïŋ―ïŋ― 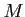 ïŋ―ØĪΚïŋ―ïŋ―ŅĪÏĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―ÖĪĮļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÖĨïŋ―ïŋ―ïŋ―ïŋ―饞ïŋ―ÜĄŨĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―šÝĪËĪÏĪïŋ―ïŋ―ĘĪęīķïŋ―ÐĪïŋ―ïŋ―ÛĪĘĪïŋ―ïŋ―įĪŽïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ØĪΚïŋ―ïŋ―ŅĪÏĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―ÖĪĮļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÖĨïŋ―ïŋ―ïŋ―ïŋ―饞ïŋ―ÜĄŨĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―šÝĪËĪÏĪïŋ―ïŋ―ĘĪęīķïŋ―ÐĪïŋ―ïŋ―ÛĪĘĪïŋ―ïŋ―įĪŽïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ― 3.1 (ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―Į§)
ïŋ―ïŋ―
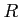
ïŋ―ïŋ―Ãąïŋ―Ėļïŋ―ïŋ―ïŋ―
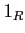
ïŋ―Č―ņĪŊĪÎĪĮĪïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ïŋ―
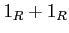
ïŋ―ïŋ―
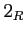
,
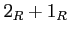
ïŋ―ïŋ―
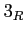
ïŋ―ïŋ―ïŋ―Č―ņĪŊĄïŋ―
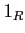
ïŋ―ïŋ―
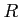
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÞĨïŋ―ïŋ―ĘĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
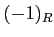
,
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ïŋ―
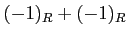
ïŋ―ïŋ―
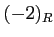
ïŋ―ïŋ―ïŋ―Č―ņĪŊĄïŋ―
ïŋ―ïŋ― 3.3
ïŋ―ïŋ―
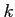
ïŋ―ïŋ―ΰïŋ―ÄĪÎđïŋ―ïŋ―ïŋ―
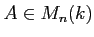
ïŋ―ïŋ―ïŋ―ïŋ―ęĪđïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―
Âŋïŋ―āž°ïŋ―ïŋ―
![$ k[X]$](img19.png)
ïŋ―ïŋ―
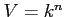
ïŋ―ØĪΚïŋ―ïŋ―ŅĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÞĪëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 3.1
![$ k[X]$](img19.png)
ïŋ―ïŋ―
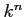
ïŋ―ØĪΚïŋ―ïŋ―ŅĪĮĪïŋ―ïŋ―ÃĪÆĄïŋ―
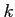
ïŋ―Κïŋ―ïŋ―ŅĪïŋ―
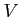
ïŋ―Îļïŋ―ïŋ―ÎĨïŋ―ïŋ―ïŋ―ïŋ―饞ïŋ―ÜĪïŋ―
ïŋ―ïŋ―ïŋ―ŨĪïŋ―ïŋ―ïŋ―čĪĶïŋ―ĘĪïŋ―ÎĪÏĄïŋ―ïŋ―ïŋ―ËĩóĪēĪïŋ―ïŋ―ïŋ―ÎĪËļÂĪëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ― 3.4
ïŋ―ïŋ―
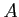
ïŋ―Č·ïŋ―
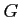
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ėĪŋïŋ―ČĪïŋ―ïŋ―ïŋ―
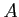
ïŋ―ïŋ―ïŋ―
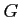
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― ![$ A[G]$](img25.png)
ïŋ―ČĪÏĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―Íïŋ―ïŋ―ïŋ―ÂĪÎ―ïŋ―ïŋ―ïŋ―
ïŋ―Ë·ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ÂĄïŋ―ïŋ―ŅĪïŋ―Æģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢ
(ïŋ―ïŋ―
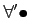 ïŋ―ïŋ― ïŋ―ÏĄïŋ―Íïŋ―ÂļÄĪïŋ―ïŋ―ãģ°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―
ïŋ―ïŋ― ïŋ―ÏĄïŋ―Íïŋ―ÂļÄĪïŋ―ïŋ―ãģ°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ― 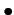 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĖĢïŋ―ĮĪïŋ―ïŋ―ëĄĢ)
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĖĢïŋ―ĮĪïŋ―ïŋ―ëĄĢ)
ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ËĪÏĄïŋ―ïŋ―ÂĄïŋ―ïŋ―ŅĪÏžïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
-
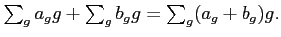
-
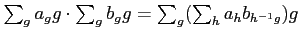
ïŋ―ïŋ―ïŋ― 3.5
ïŋ―ïŋ―
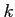
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―
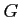
ïŋ―ïŋ―
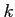
ïŋ―ïŋ―ïŋ―
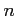
-ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―
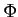
ïŋ―ČĪÏĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―
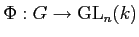
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ČĪĮĪïŋ―ïŋ―ëĄĢ
Ėŋïŋ―ïŋ― 3.6
ïŋ―ïŋ―
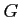
ïŋ―ïŋ―
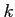
ïŋ―ïŋ―ïŋ―
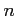
-ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―
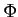
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ėĪŋïŋ―ČĪïŋ―ïŋ―ïŋ―
![$ A[G]$](img25.png)
ïŋ―ïŋ―
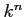
ïŋ―ØĪΚïŋ―ïŋ―ŅĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÞĪëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 3.2
5ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
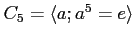
ïŋ―Îūïŋ―ïŋ―
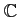
ïŋ―ïŋ―ηïŋ―ïŋ―ïŋ―
![$ {\mathbb{C}}[C_5]$](img37.png)
ïŋ―Ξïŋ―ïŋ―ηŨŧïŋ―ïŋ―ōĪ·Īïŋ―ïŋ―čĄĢ(ïŋ―ïŋ―ïŋ―ÏĪĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ãąïŋ―ËĪïŋ―ïŋ―ëĪģïŋ―ČĄïŋ―)



Next: About this document ...
2010-04-20
![]()
![]() -ïŋ―÷ïŋ―
-ïŋ―÷ïŋ― ![]() ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―![]() ïŋ―Îļïŋ―ïŋ―ïŋ―
ïŋ―Îļïŋ―ïŋ―ïŋ― ![]() ïŋ―ØĪΚïŋ―ïŋ―ŅĪÏĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―ÖĪĮļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÖĨïŋ―ïŋ―ïŋ―ïŋ―饞ïŋ―ÜĄŨĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―šÝĪËĪÏĪïŋ―ïŋ―ĘĪęīķïŋ―ÐĪïŋ―ïŋ―ÛĪĘĪïŋ―ïŋ―įĪŽïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ØĪΚïŋ―ïŋ―ŅĪÏĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―ÖĪĮļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÖĨïŋ―ïŋ―ïŋ―ïŋ―饞ïŋ―ÜĄŨĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―šÝĪËĪÏĪïŋ―ïŋ―ĘĪęīķïŋ―ÐĪïŋ―ïŋ―ÛĪĘĪïŋ―ïŋ―įĪŽïŋ―ïŋ―ïŋ―ëĄĢ
![% latex2html id marker 895
$\displaystyle A[G]=
\left\{
\sum_{g \in G} a_g g \ ; \qquad a_g=0 \quad \forall' g \in G
\right\}
$](img26.png)