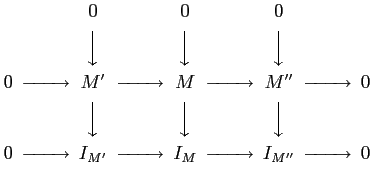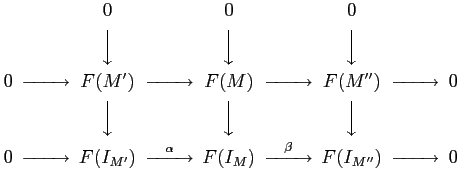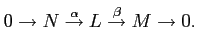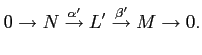Next: Bibliography
Cohomologies.
Yoshifumi Tsuchimoto
 We recommend the book of Lang [1] as a good reference.
The treatment here follows the book for the most part.
We recommend the book of Lang [1] as a good reference.
The treatment here follows the book for the most part.
THEOREM 07.1
Let
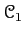 be an abelian category with enough injectives, and let
be an abelian category with enough injectives, and let
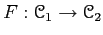 be a covariant additive left functor to another abelian
category
be a covariant additive left functor to another abelian
category
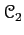 . Then:
. Then:
-
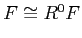 .
.
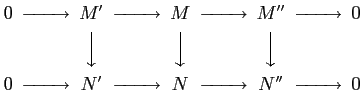
- For each short exact sequence
and for each 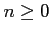 there is a natural homomorphism
there is a natural homomorphism
such that we obtain a long exact sequence
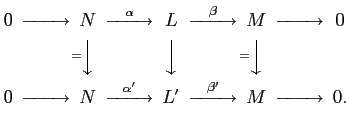
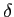 is natural. That means, for a morphism of short exact sequences
is natural. That means, for a morphism of short exact sequences
the 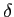 's give a commutative diagram:
's give a commutative diagram:
- For each injective objective object
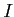 of
of 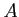 and for each
and for each 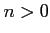 we have
we have 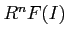 .
.
The collection 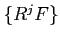 of functors
of functors 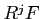 is a ``universal delta functor''. See [1].
is a ``universal delta functor''. See [1].
LEMMA 07.2
Under the assumption of the previous theorem,
for any exact sequence
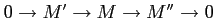 of objects in
of objects in
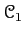 ,
there exists injective resolutions
,
there exists injective resolutions
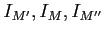 of
of 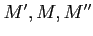 respectively and a commutative diagram
respectively and a commutative diagram
such that the diagram of resolutions is exact.
Thus we obtain a diagram
such that each row in the last line is exact.
Note that 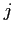 -th cohomology of the complex
-th cohomology of the complex
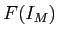 (respectively,
(respectively,
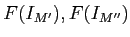 )
gives the
)
gives the
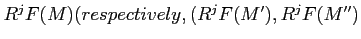 .)
Using the resolution given in the lemma above, we may prove
Theorem 7.1.
Let us describe the map
.)
Using the resolution given in the lemma above, we may prove
Theorem 7.1.
Let us describe the map 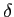 in more detail when
in more detail when
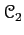 is a
category of modules by ``diagram chasing''.
Namely, for
is a
category of modules by ``diagram chasing''.
Namely, for
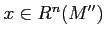 , let us show how to compute
, let us show how to compute 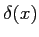 .
.
-
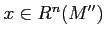 may be represented as a class
may be represented as a class ![$ [c_x]$](img30.png) of a cocycle
of a cocycle
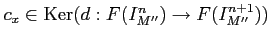 .
.
- We take a ``lift''
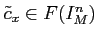 such that
such that
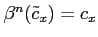 . Note that
. Note that
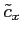 is no longer a cocycle.
is no longer a cocycle.
- Consider
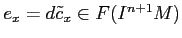 .
It is a coboundary and we have
.
It is a coboundary and we have
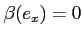 .
.
- There thus exists an element
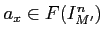 such that
such that
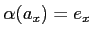 .
. 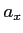 is no longer a coboundary but it is a cocycle.
is no longer a coboundary but it is a cocycle.
- The cohomology class
![$ [a_x]$](img40.png) of
of 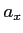 is the required
is the required 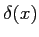 .
.
Such computation appears frequently when we deal with cohomologies.
DEFINITION 07.3
Let
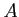
be a ring. Let
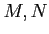
be
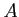
-modules. Then an
extension
of
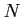
by
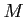
is a module
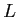
with a exact sequence
|
(E) |
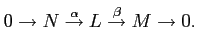 |
of
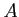
-modules.
Let
be another extension. Then the two extensions are said to be isomorphic
if there exists a commutative diagram
See [1, XX,Exercise 27]



Next: Bibliography
2010-06-15
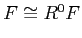 .
.
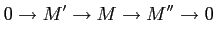
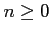 there is a natural homomorphism
there is a natural homomorphism
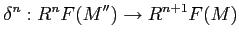
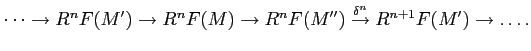
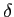 is natural. That means, for a morphism of short exact sequences
is natural. That means, for a morphism of short exact sequences
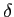 's give a commutative diagram:
's give a commutative diagram:
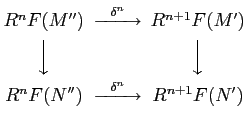
 of
of 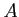 and for each
and for each 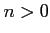 we have
we have 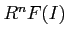 .
.