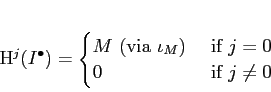Next: Bibliography
Cohomologies.
Yoshifumi Tsuchimoto
By employing the following axiom
instead of the axiom (functor-2) above, we obtain a definition of
a contravariant functor:
(functor-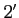 )
)
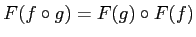 for any composable morphisms
for any composable morphisms
DEFINITION 05.2
Let
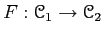
be a functor between additive categories.
We call
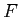 additive
additive if for any objects
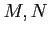
in
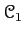
,
is additive.
DEFINITION 05.3
Let
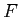
be an additive functor from an abelian category
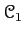
to
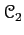
.
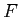 is said to be left exact (respectively, right exact )
if for any exact sequence
is said to be left exact (respectively, right exact )
if for any exact sequence
the corresponding map
(respectively,
is exact
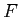 is said to be exact if it is both left exact and right exact.
is said to be exact if it is both left exact and right exact.
LEMMA 05.4
Let 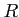 be a (unital associative but not necessarily commutative) ring.
Then for any
be a (unital associative but not necessarily commutative) ring.
Then for any 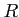 -module
-module 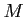 , the following conditions are equivalent.
, the following conditions are equivalent.
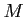 is a direct summand of free modules.
is a direct summand of free modules.
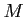 is projective
is projective
COROLLARY 05.5
For any ring 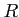 , the category
, the category
 of
of 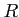 -modules
have enough projectives. That means, for any object
-modules
have enough projectives. That means, for any object
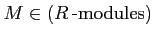 ,
there exists a projective object
,
there exists a projective object 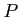 and a surjective morphism
and a surjective morphism
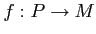 .
.
DEFINITION 05.6
Let
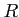
be a commutative ring.
We assume
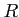
is a domain (that means,
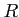
has no zero-divisors except for 0
.)
An 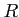 -module
-module 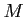 is said to be divisible if
for any
is said to be divisible if
for any
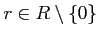 , the multplication map
, the multplication map
is surjective.
DEFINITION 05.7
Let
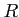
be a commutative ring.
We assume
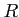
is a domain (that means,
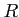
has no zero-divisors except for 0
.)
An 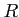 -module
-module 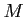 is said to be divisible if
for any
is said to be divisible if
for any
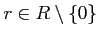 , the multplication map
, the multplication map
is epic.
DEFINITION 05.8
Let
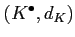
,
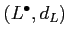
be complexes of objects
of an additive category
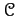
.
- A morphism of complex
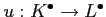 is a family
is a family
of morphisms in
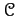 such that
such that 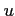 commutes with
commutes with 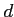 . That means,
. That means,
holds.
- A homotopy between two morphisms
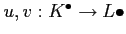 of complexes is a family of morphisms
of complexes is a family of morphisms
such that
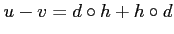 holds.
holds.
DEFINITION 05.10
Let
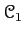
be an abelian category which has enough injectives.
Let
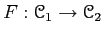
be a left exact functor to an abelian category.
Then for any object
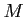
of
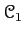
we take an injective resolution
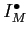
of
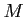
and define
and call it the derived functor of
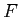
.
LEMMA 05.11
The derived functor is indeed a functor.



Next: Bibliography
2010-05-27
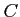 of
of
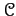 an object
an object 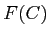 of
of
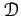 .
.
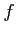 of
of
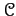 an morphism
an morphism 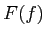 of
of
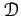 .
.
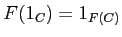 for any object
for any object 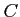 of
of
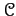 .
.
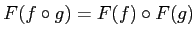 for any composable morphisms
for any composable morphisms
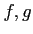 of
of
 .
.
![]() )
)
![]() for any composable morphisms
for any composable morphisms
![]() -module
-module ![]() is said to be divisible if
for any
is said to be divisible if
for any
![]() , the multplication map
, the multplication map
![]() -module
-module ![]() is said to be divisible if
for any
is said to be divisible if
for any
![]() , the multplication map
, the multplication map