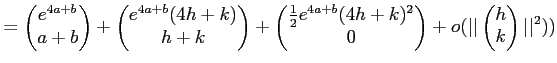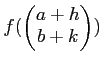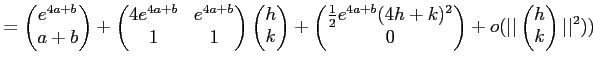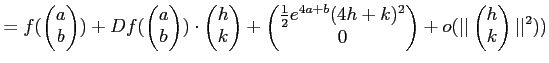Next: About this document ...
ïŋ―ïŋ―ïŋ―Ïģïŋ― IA ïŋ―îļģïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĘĪßĪïŋ―  ïŋ―Ïžïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ΰïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―Ïžïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ΰïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―Ðŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪÃĪÆĪïŋ―ïŋ―ėĪĪïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÞĨïŋ―ïŋ―ïŋ―):
ïŋ―ïŋ―ĖĪËĪÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―6F ïŋ―ïŋ―ïŋ―Ø·Įžïŋ―ïŋ―ÄĪĮđÔĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Î―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―3ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ė―ĩïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Í―ïŋ―ęĄĢïŋ―Įžïŋ―ïŋ―ÞĪĮĪïŋ―
ïŋ―ïŋ―ïŋ―ÓĪËĪÄĪïŋ―ïŋ―ÆĪΞïŋ―ïŋ―ïŋ―ËĪÏ°ïŋ―ïŋ―Úąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
(1)
(2)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―ïŋ―Îđïŋ―ïŋ―óž°Īïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
(3)
ïŋ―ïŋ―ïŋ―óžĄķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŨĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪÏĪïŋ―ïŋ―ïŋ―Į―ïŋ―ĘŽïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―âĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ėĨĪïŋ―Ę―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ęēïŋ―ïŋ―Ë―ņĪĪĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―) ïŋ―ïŋ―  ïŋ―ïŋ―
ïŋ―ïŋ―  ïŋ―ĮĪïŋ―ïŋ―ÍĪĮĪïŋ―ïŋ―ęĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ėžĄïŋ―Îđïŋ―)ïŋ―ÏĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ÍĪĮĪïŋ―ïŋ―ęĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ėžĄïŋ―Îđïŋ―)ïŋ―ÏĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 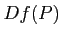 ïŋ―ËĪïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―Į°ïŋ―ĘĪïŋ―ïŋ―éĄĒïŋ―óžĄĪÎđïŋ―ËĪÄĪïŋ―ïŋ―ÆĪÏĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÛĪÉīïŋ―ïŋ―ØĪĘ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪĘĪïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æļïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―ïŋ―ÖĨÆĨóĨ―Ĩëŧŧïŋ―ŨĪïŋ―
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ëĄĢ)ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―óžĄĪÎđïŋ―ËĪÄĪïŋ―ïŋ―ÆĪÏšïŋ―ïŋ―ïŋ―Îūïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ÆĪÏūïŋ―ηïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ĘŽïŋ―ïŋ―Ãąïŋ―ĮĪïŋ―ïŋ―ïŋ―ÎĪĮĄïŋ―
Åļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪâĄĒïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ÆĪïŋ―ÉĪïŋ―ïŋ―ïŋ―ĮĪïŋ―čĪĪïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―Į°ïŋ―ĘĪïŋ―ïŋ―éĄĒïŋ―óžĄĪÎđïŋ―ËĪÄĪïŋ―ïŋ―ÆĪÏĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÛĪÉīïŋ―ïŋ―ØĪĘ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪĘĪïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æļïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―ïŋ―ÖĨÆĨóĨ―Ĩëŧŧïŋ―ŨĪïŋ―
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ëĄĢ)ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―óžĄĪÎđïŋ―ËĪÄĪïŋ―ïŋ―ÆĪÏšïŋ―ïŋ―ïŋ―Îūïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ÆĪÏūïŋ―ηïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ĘŽïŋ―ïŋ―Ãąïŋ―ĮĪïŋ―ïŋ―ïŋ―ÎĪĮĄïŋ―
Åļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪâĄĒïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ÆĪïŋ―ÉĪïŋ―ïŋ―ïŋ―ĮĪïŋ―čĪĪïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îēïŋ―ïŋ―ïŋ―ïŋ―ōļŦĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―čĪĶïŋ―ËĄïŋ―(1) ïŋ―ïŋ―(2)ïŋ―ïŋ― 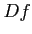 ïŋ―ïŋ―ïŋ―ïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―ōļŦĪïŋ―ïŋ―
ïŋ―čĪĪ(ïŋ―ÕĪËļïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―(2)ïŋ―ïŋ―ïŋ―ïŋ―Čūïŋ―ïŋ―(1)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ãąïŋ―ïŋ―ïŋ―ÂĪŲĪïŋ―ïŋ―ïŋ―ÉĪïŋ―)ïŋ―ïŋ―ïŋ―ïŋ―
(3)ïŋ―ΰėžĄïŋ―Îđïŋ―ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÐĄïŋ―(1)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(2)ïŋ―ïŋ―ïŋ―ïŋ―Čūïŋ―ïŋ―ïŋ―ïŋ―Æ°ÅŠïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―ōļŦĪïŋ―ïŋ―
ïŋ―čĪĪ(ïŋ―ÕĪËļïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―(2)ïŋ―ïŋ―ïŋ―ïŋ―Čūïŋ―ïŋ―(1)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ãąïŋ―ïŋ―ïŋ―ÂĪŲĪïŋ―ïŋ―ïŋ―ÉĪïŋ―)ïŋ―ïŋ―ïŋ―ïŋ―
(3)ïŋ―ΰėžĄïŋ―Îđïŋ―ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÐĄïŋ―(1)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(2)ïŋ―ïŋ―ïŋ―ïŋ―Čūïŋ―ïŋ―ïŋ―ïŋ―Æ°ÅŠïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
(4)
ïŋ―Ņŋïŋ―ïŋ―Ņīïŋ―ïŋ―Įĩïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ÐĪĘĪïŋ―ĘĪïŋ―ïŋ―ÎĪÏĄïŋ―
- ïŋ―ΰïŋ―ïŋ―ïŋ―Ņīïŋ― (
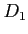 ïŋ―ïŋ―
ïŋ―ïŋ― 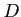 ïŋ―ËĄïŋ―)
ïŋ―ËĄïŋ―)
- ïŋ―ïŋ―ĘŽïŋ―Øŋïŋ―ïŋ―ïŋ―ïŋ―Ņīïŋ―(
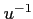 ïŋ―ïŋ―
ïŋ―ïŋ―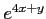 ïŋ―ËĄïŋ―)
ïŋ―ËĄïŋ―)
- ÂŽïŋ―ŲĪïŋ―ïŋ―Ņīïŋ―(
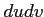 ïŋ―ïŋ―
ïŋ―ïŋ―
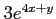 ïŋ―ËĄïŋ―)
ïŋ―ËĄïŋ―)
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
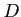 ïŋ―ïŋ―
ïŋ―ïŋ―  ïŋ―ïŋ―
ïŋ―ïŋ―  ïŋ―Į°ïŋ―ïŋ―аïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪÏĄïŋ―
ïŋ―Į°ïŋ―ïŋ―аïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪÏĄïŋ― ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―
 ïŋ―ÎĩÕžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ïŋ―ïŋ―Æ°ŨĪËžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ĖĢïŋ―ÎĪïŋ―ïŋ―ïŋ―ÔĪÏĪïŋ―ÃĪÆĪßĪïŋ―ČĪčĪĪïŋ―ïŋ―
ïŋ―ÎĩÕžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ïŋ―ïŋ―Æ°ŨĪËžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ĖĢïŋ―ÎĪïŋ―ïŋ―ïŋ―ÔĪÏĪïŋ―ÃĪÆĪßĪïŋ―ČĪčĪĪïŋ―ïŋ―



Next: About this document ...
2009-07-31
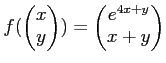
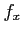 ,
, 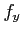 ïŋ―ōĪ―ĪėĪūïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ōĪ―ĪėĪūïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―  ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽ
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽ
 (ïŋ―ÉĪïŋ―ïŋ―ïŋ―Î―ïŋ―ïŋ―ïŋ―ïŋ―Į―ņĪĪĪÆĪïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ĖĢïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―Îđïŋ―ïŋ―ïŋ―
(ïŋ―ÉĪïŋ―ïŋ―ïŋ―Î―ïŋ―ïŋ―ïŋ―ïŋ―Į―ņĪĪĪÆĪïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ĖĢïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―Îđïŋ―ïŋ―ïŋ―
 ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―  ïŋ―ïŋ―ïŋ―óžĄķïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―óžĄķïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![$\displaystyle D=[0,1] \times [0,1]
$](img12.png)
 ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
 ïŋ―ïŋ―
ïŋ―ïŋ―
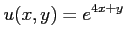
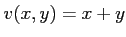
 ïŋ―ËĪïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―  ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 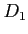 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―
ïŋ―ïŋ―Ãąïŋ―ÍĪïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪÏūïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―Ëžïŋ―Íģïŋ―ËŧČĪÃĪÆĪčĪĪïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ëĄĢ)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―
ïŋ―ïŋ―Ãąïŋ―ÍĪïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪÏūïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―Ëžïŋ―Íģïŋ―ËŧČĪÃĪÆĪčĪĪïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ëĄĢ)
![\includegraphics[scale=0.5]{mondai.eps}](img19.png)
![\includegraphics[scale=0.5]{mondai1.eps}](img20.png)