![]() ¿�ѿ��ؿ���(��ޥ�)��ʬ(5) �ѿ��Ѵ�(�ĤŤ�)��
¿�ѿ��ؿ���(��ޥ�)��ʬ(5) �ѿ��Ѵ�(�ĤŤ�)��
�ѿ��Ѵ�
![\includegraphics[scale=0.5]{14a.eps}](img13.png)
![\includegraphics[scale=0.5]{14b.eps}](img14.png)
�����ʶ��Ĺ����
![]() ��Ǥ�
����Ѵ��Ϥ�����������Ѵ�
��Ǥ�
����Ѵ��Ϥ�����������Ѵ�
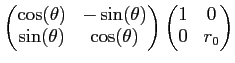
�Ƕ�����졢��äƤ������Ѥ��Ѵ��ˤ�äƤۤ�
�����ʬ
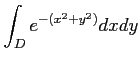
������
�����ʬ
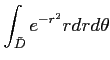
�Ȥʤ롣������ưפ�(����ʬ�ˤ��)��ʬ���������
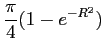
�Ǥ��롣 ���Τ��Ȥϰ��ѿ�����ʬ�ˤ���Ѥ���ơ�
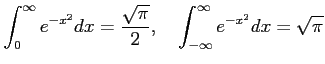
�����롣
�ѿ��Ѵ��ΰ켡�����Jacobian, ��ʬ���ѿ��Ѵ�����Ʋ�˲� �����դ��������ˤʤ�Ǥ���������������ͤ����� �ɤ��ȤˤĤ��Ƥ������ȡ�