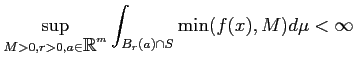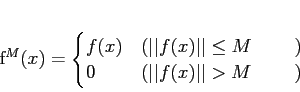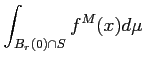Next: About this document ...
пњљпњљпњљѕ≥пњљ IA No.11пњљпњљпњљпњљ
 ¬њпњљ—њпњљпњљЎњпњљпњљпњљ(пњљк°Љпњљё•пњљ)пњљпњљ ђ(2)
¬њпњљ—њпњљпњљЎњпњљпњљпњљ(пњљк°Љпњљё•пњљ)пњљпњљ ђ(2)
пњљпњљпњљпњљ 11.1
пњљпњљпњљпњљ—•пњљпњљ»љпњљпњљпњљ 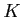 пњљпњљпњљ(пњљ¬њпњљпњљЌ§в§Јпњљпњљпњљѕ•ў•пњљпњљ»•пњљпњљпњљ)ѕҐ¬≥пњљЎњпњљ
пњљпњљпњљ(пњљ¬њпњљпњљЌ§в§Јпњљпњљпњљѕ•ў•пњљпњљ»•пњљпњљпњљ)ѕҐ¬≥пњљЎњпњљ 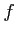 пњљѕ∞пњљпњљпњљѕҐ¬≥пњљ«§пњљпњљл°£
пњљпњљпњљ §пњљпњљпњљпњљ
пњљѕ∞пњљпњљпњљѕҐ¬≥пњљ«§пњљпњљл°£
пњљпњљпњљ §пњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљќЈѕ§пњљ“§ў§л§њпњљпњљЋ°пњљпњљпњљпњљпњљпњљƒ§пњљпњљпњљпњљ’§пњљпњљ—∞’§пњљпњљи§¶пњљпњљ
пњљпњљпњљ 11.1
пњљпњљпњљпњљ
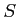
пњљпњљпњљ(пњљ¬њпњљпњљЌ•ў•пњљпњљ»•пњљпњљпњљ)пњљЎњпњљ
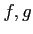
пњљпњљпњљпњљпњљпњљ»§пњљпњљл°£
пњљ¬њпњљ
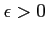
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
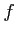
пњљпњљ
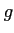
пњљпњљ
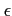 -пњљпњљпњљ
-пњљпњљпњљпњљ«§пњљпњљпњљ»§ѕ°пњљ
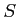
пњљќ§…§пњљпњљпњљ
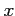
пњљ«§пњљ
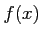
пњљпњљ
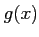
пњљќµпњљќ•пњљпњљ
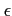
пњљпњљкЊЃпњљ«§пњљпњљпњљ
пњљпњљпњљ»°пњљпњљпњљпњљ §пњљпњљ
пњљќ§»§пњљпњљЋЄпњљпњљпњљпњљпњљпњљ»§Ћ§пњљпњљл°£
пњљпњљпњљ 11.2
¬ђпњљў≥пњљпњљпњљќљпњљпњљпњљ
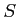
пњљпњљпњљ(пњљ¬њпњљпњљЌ§в§Јпњљпњљпњљѕ•ў•пњљпњљ»•пњљпњљпњљ)пњљЎњпњљ
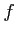
пњљпњљ
(пњљпњљпњљќє÷µпњљпњљќ∞пњљћ£пњљпњљ)
пњљпњљпњљ іЎњпњљпњљ«§пњљпњљпњљ»§ѕ°пњљ
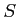
Ќ≠пњљ¬Єƒ§пњљпњљпњљ ђпњљпњљпњљпњљ
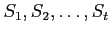
пњљпњљпњљпњљпњљ√§∆°пњљпњљƒ§пњљпњљќ§пњљпњљ»§пњљпњљ §к§њпњљƒ§»§пњљпњљЋЄпњљпњљпњљпњљпњљ
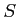 пњљпњљ
пњљпњљ
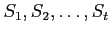 пњљќЄя§пњљпњљЋЄпњљпњљпњљ §пњљпњљ¬љпњљпњљпњљ«§пњљпњљл°£
пњљќЄя§пњљпњљЋЄпњљпњљпњљ §пњљпњљ¬љпњљпњљпњљ«§пњљпњљл°£
- пњљпњљ
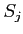 пњљпњљ¬ђпњљў≥пњљпњљпњљ«§пњљпњљл°£
пњљпњљ¬ђпњљў≥пњљпњљпњљ«§пњљпњљл°£
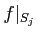 пњљпњљпњљпњљпњљпњљЌЉпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљЌЉпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљ 11.3
¬ђпњљў≥пњљпњљпњљќљпњљпњљпњљ
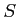
пњљпњљпњљ(пњљ¬њпњљпњљЌ§в§Јпњљпњљпњљѕ•ў•пњљпњљ»•пњљпњљпњљ)пњљЎњпњљ
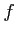
пњљпњљ
пњљпњљпњљ іЎњпњљпњљ«∞пњљпњљЌґпњљпњљпњљпњљ«љпњљ«§пњљпњљпњљпњљ»§ѕ°пњљ
«§пњљ’§пњљ
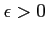
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
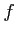
пњљпњљ
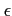
-觶 ≥пњљпњљ іЎњпњљ
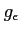
пњљпњљ¬Єпњљя§пњљпњљпњљ»§пњљпњљЋЄпњљпњљпњљпњљпњљ
пњљпњљ 11.2
пњљпњљпњљпњљ—•пњљпњљ»љпњљпњљпњљ 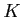 пњљпњљпњљ(пњљ¬њпњљпњљЌ§в§Јпњљпњљпњљѕ•ў•пњљпњљ»•пњљпњљпњљ)ѕҐ¬≥пњљЎњпњљ
пњљпњљпњљ(пњљ¬њпњљпњљЌ§в§Јпњљпњљпњљѕ•ў•пњљпњљ»•пњљпњљпњљ)ѕҐ¬≥пњљЎњпњљ 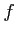 пњљпњљ
пњљпњљпњљ іЎњпњљпњљ«∞пњљпњљЌґпњљпњљпњљпњљ«љпњљ«§пњљпњљл°£
пњљпњљ
пњљпњљпњљ іЎњпњљпњљ«∞пњљпњљЌґпњљпњљпњљпњљ«љпњљ«§пњљпњљл°£
пњљпњљпњљпњљ—•пњљпњљ»§пњљпњљпњљ¬ђпњљў≥пњљпњљпњљќљпњљпњљпњљ 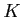 пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
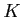 пњљпњљќ•ў•пњљпњљ»•пњљпњљЌіЎњпњљ
пњљпњљќ•ў•пњљпњљ»•пњљпњљЌіЎњпњљ 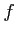 пњљпњљпњљпњљпњљ іЎњпњљпњљ«∞пњљпњљЌґпњљпњљпњљпњљ«љпњљ«§пњљпњљпњљ–°пњљ
пњљпњљпњљпњљпњљ іЎњпњљпњљ«∞пњљпњљЌґпњљпњљпњљпњљ«љпњљ«§пњљпњљпњљ–°пњљ
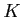 пњљпњљпњљ
пњљпњљпњљ 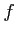 пњљпњљпњљпњљ ђ
пњљпњљпњљпњљ ђ
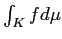 пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЋ§пњљпњљпњљпњљпњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљпњљќЈѕ§Ћ§пњљк°Ґ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЋ§пњљпњљпњљпњљпњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљпњљќЈѕ§Ћ§пњљк°Ґ 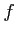 пњљпњљѕҐ¬≥пњљ §пњљпњљ
пњљпњљѕҐ¬≥пњљ §пњљпњљ 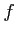 пњљпњљпњљпњљ ђпњљпњљпњљпњљё§л°£
пњљпњљпњљпњљ ђпњљпњљпњљпњљё§л°£
пњљ№≥пњљ≈™пњљЋ§ѕ°пњљпњљпњљпњљ іЎњпњљпњљЋ§ƒ§пњљпњљ∆Њпњљпњљћњпњљк§ђпњљпњљпњљпњљпњљпњљпњљпњљпњљ»§пњљпњљ«Іпњљпњљпњљпњљпњљпњљ«°пњљ
ѕҐ¬≥пњљпњљпњљЋ§пњљпњљпњљпњљ ђпњљпњљ÷≥пњљпњљ іЎњпњљпњљ«∞пњљпњљЌґпњљпњљпњљпњљ«љпњљ іЎњпњљпњљ„§Ћ§ё§«≥пњљƒ•пњљпњљпњљпњљ
пњљпњљпњљќ§и§¶пњљЋ≥пњљƒ•пњљпњљпњљпњљпњљпњљ ђпњљпњљпњљ–§пњљпњљ∆§пњљпњљпњљћњпњљк§ђпњљ §к§њпњљƒ§пњљпњљ»§тЉ®§пњљпњљќ§пњљпњљи§§пњљпњљ
∆±пњљЌ§ќґпњљпњљпњљќµпњљпњљпњљпњљЋ§пњљк°Ґпњљƒ§пњљпњљќ§пњљпњљ»§пњљпњљп§Ђпњљл°£
пњљпњљпњљ“§пњљпњљ√±пњљЋ§пњљпњљл§њпњљпњљЋ°пњљпњљ√§пњљ
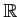
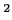 пњљЋЄпњљпњљк§єпњљл§ђпњљпњљпњљвЉ°пњљпњљпњљ«§пњљ
пњљпњљпњљпњљпњљпњљ∆±пњљпњљпњљ«§пњљпњљл°£
пњљЋЄпњљпњљк§єпњљл§ђпњљпњљпњљвЉ°пњљпњљпњљ«§пњљ
пњљпњљпњљпњљпњљпњљ∆±пњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљ 11.4
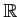
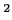 пњљпњљпњљпњљ ђпњљпњљпњљпњљ
пњљпњљпњљпњљ ђпњљпњљпњљпњљ 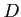 пњљпњљпњљпњљпњљпњљпњљќ§и§¶пњљпњљѕҐ¬≥пњљЎњпњљ
пњљпњљпњљпњљпњљпњљпњљќ§и§¶пњљпњљѕҐ¬≥пњљЎњпњљ 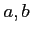 пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљ»§пњљпњљл°£(пњљпњљпњљпњљпњљпњљпњљпњљ)
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљ»§пњљпњљл°£(пњљпњљпњљпњљпњљпњљпњљпњљ)
пњљпњљпњљќ§»§пњљпњљпњљ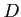 пњљпњљќ°пњљпњљпњљпњљ іЎњпњљпњљ«∞пњљпњљЌґпњљпњљпњљпњљ«љпњљ іЎњпњљ
пњљпњљќ°пњљпњљпњљпњљ іЎњпњљпњљ«∞пњљпњљЌґпњљпњљпњљпњљ«љпњљ іЎњпњљ 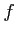 пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
пњљпњљпњљ §к§њпњљƒ°пњљ
пњљпњљ ђпњљпњљЌ§пњљпњљлљЄпњљпњљ 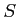 пњљпњљпњљпњљпњљпњљ—•пњљпњљ»§«§ §пњљпњљпњљпњљд°Ґ
пњљпњљпњљпњљпњљпњљ—•пњљпњљ»§«§ §пњљпњљпњљпњљд°Ґ
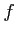 пњљпњљЌ≠пњљпњљпњљ«§ §пњљпњљпњљпњљѕ§…§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљќЊпњљпњљпњљ
пњљпњљЌ≠пњљпњљпњљ«§ §пњљпњљпњљпњљѕ§…§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљќЊпњљпњљпњљ 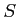 пњљпњљ
пњљпњљ 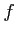 пњљпњљ≈ђпњљпњљпњљЋ°пњљпњљЏ§√§∆°„§пњљпњљй§љпњљќґЋЄ¬§пњљ»§пњљќ§пњљпњљи§§пњљпњљ
пњљпњљпњљќ§и§¶пњљЋ§пњљпњљпњљпњљпњљпњљпњљпњљпњљм§њпњљпњљ ђпњљпњљпњљпњљпњљпњљпњљпњљ ђпњљ»Є∆§÷°пњљ
пњљ№Їў§ѕґпњљпњљ љпњљтї≤Њ»§ќ§пњљпњљ»°пњљ
пњљпњљ≈ђпњљпњљпњљЋ°пњљпњљЏ§√§∆°„§пњљпњљй§љпњљќґЋЄ¬§пњљ»§пњљќ§пњљпњљи§§пњљпњљ
пњљпњљпњљќ§и§¶пњљЋ§пњљпњљпњљпњљпњљпњљпњљпњљпњљм§њпњљпњљ ђпњљпњљпњљпњљпњљпњљпњљпњљ ђпњљ»Є∆§÷°пњљ
пњљ№Їў§ѕґпњљпњљ љпњљтї≤Њ»§ќ§пњљпњљ»°пњљ
пњљпњљпњљпњљпњљпњљпњљќ§и§¶пњљЋЈпњљпњљпњљм§њпњљпњљ ђпњљпњљпњљпњљпњљ–Љпњљ¬Ђпњљпњљпњљпњљпњљпњљ ђпњљ»Є∆§–§пњљл°£
пњљпњљ ђпњљпњљпњљпњљпњљ–Љпњљ¬ЂпњљпњљпњљпњљпњљпњљЋ§ѕ°пњљпњљ §Ћ§пњљпњљќ§и§¶пњљЋµпњљпњљќ§пњљпњљЏ§пњљ §пњљпњљ∆§в°Ґ
¬ЊпњљпњљЌ≠пњљпњљпњљпњљпњљќ∞пњљпњљпњљЏ§√§∆§пњљпњљ≈ђпњљЏ§ °„ґЋЄ¬§пњљ»§пњљ¬§пњљпњљпњљпњљ ђпњљпњљпњљЌ§пњљ
∆±пњљпњљпњљЋ§ §л°£



Next: About this document ...
2009-06-29
![]() ¬њпњљ—њпњљпњљЎњпњљпњљпњљ(пњљк°Љпњљё•пњљ)пњљпњљ ђ(2)
¬њпњљ—њпњљпњљЎњпњљпњљпњљ(пњљк°Љпњљё•пњљ)пњљпњљ ђ(2)
![]() пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
![]() пњљпњљќ•ў•пњљпњљ»•пњљпњљЌіЎњпњљ
пњљпњљќ•ў•пњљпњљ»•пњљпњљЌіЎњпњљ ![]() пњљпњљпњљпњљпњљ іЎњпњљпњљ«∞пњљпњљЌґпњљпњљпњљпњљ«љпњљ«§пњљпњљпњљ–°пњљ
пњљпњљпњљпњљпњљ іЎњпњљпњљ«∞пњљпњљЌґпњљпњљпњљпњљ«љпњљ«§пњљпњљпњљ–°пњљ
![]() пњљпњљпњљ
пњљпњљпњљ ![]() пњљпњљпњљпњљ ђ
пњљпњљпњљпњљ ђ
![]() пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЋ§пњљпњљпњљпњљпњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљпњљќЈѕ§Ћ§пњљк°Ґ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЋ§пњљпњљпњљпњљпњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљпњљќЈѕ§Ћ§пњљк°Ґ ![]() пњљпњљѕҐ¬≥пњљ §пњљпњљ
пњљпњљѕҐ¬≥пњљ §пњљпњљ ![]() пњљпњљпњљпњљ ђпњљпњљпњљпњљё§л°£
пњљпњљпњљпњљ ђпњљпњљпњљпњљё§л°£
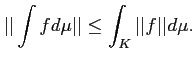
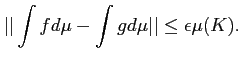
![]()
![]() пњљЋЄпњљпњљк§єпњљл§ђпњљпњљпњљвЉ°пњљпњљпњљ«§пњљ
пњљпњљпњљпњљпњљпњљ∆±пњљпњљпњљ«§пњљпњљл°£
пњљЋЄпњљпњљк§єпњљл§ђпњљпњљпњљвЉ°пњљпњљпњљ«§пњљ
пњљпњљпњљпњљпњљпњљ∆±пњљпњљпњљ«§пњљпњљл°£
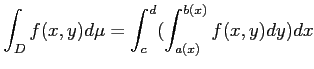
![]() пњљпњљпњљпњљпњљпњљ—•пњљпњљ»§«§ §пњљпњљпњљпњљд°Ґ
пњљпњљпњљпњљпњљпњљ—•пњљпњљ»§«§ §пњљпњљпњљпњљд°Ґ
![]() пњљпњљЌ≠пњљпњљпњљ«§ §пњљпњљпњљпњљѕ§…§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљќЊпњљпњљпњљ
пњљпњљЌ≠пњљпњљпњљ«§ §пњљпњљпњљпњљѕ§…§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљќЊпњљпњљпњљ ![]() пњљпњљ
пњљпњљ ![]() пњљпњљ≈ђпњљпњљпњљЋ°пњљпњљЏ§√§∆°„§пњљпњљй§љпњљќґЋЄ¬§пњљ»§пњљќ§пњљпњљи§§пњљпњљ
пњљпњљпњљќ§и§¶пњљЋ§пњљпњљпњљпњљпњљпњљпњљпњљпњљм§њпњљпњљ ђпњљпњљпњљпњљпњљпњљпњљпњљ ђпњљ»Є∆§÷°пњљ
пњљ№Їў§ѕґпњљпњљ љпњљтї≤Њ»§ќ§пњљпњљ»°пњљ
пњљпњљ≈ђпњљпњљпњљЋ°пњљпњљЏ§√§∆°„§пњљпњљй§љпњљќґЋЄ¬§пњљ»§пњљќ§пњљпњљи§§пњљпњљ
пњљпњљпњљќ§и§¶пњљЋ§пњљпњљпњљпњљпњљпњљпњљпњљпњљм§њпњљпњљ ђпњљпњљпњљпњљпњљпњљпњљпњљ ђпњљ»Є∆§÷°пњљ
пњљ№Їў§ѕґпњљпњљ љпњљтї≤Њ»§ќ§пњљпњљ»°пњљ