Next: About this document ...
���ϳ� IA No.10����
 ¿�ѿ��ؿ���(��ޥ�)��ʬ
¿�ѿ��ؿ���(��ޥ�)��ʬ
 ����ʬ����
����ʬ����
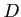 ���������줿�¿��ͤ⤷���ϥ٥��ȥ��ʹؿ�
���������줿�¿��ͤ⤷���ϥ٥��ȥ��ʹؿ� 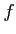 ���Ф��ơ�
���Ф��ơ�
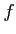 ��
�� 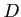 �����ʬ(����ʬ)�ϼ��Τ褦���������롣
�����ʬ(����ʬ)�ϼ��Τ褦���������롣
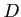 ������ʬ����
������ʬ���� 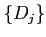 ���¤�ʬ���롣
���¤�ʬ���롣
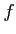 �� ��
�� �� 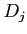 �������ʹؿ�
�������ʹؿ� 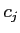 �Ƕ�����롣
�Ƕ�����롣
- ��ʬ�ͤΰ�Ĥζ���Ȥ��ơ�
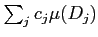 �����롣
������
�����롣
������ 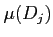 ��
�� 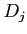 �����ѤǤ��롣
�����ѤǤ��롣
- ��ʬ
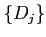 ��٤��������Ȥ�����Τ褦�ʶ������Ť��ͤ�����ʤ顢
�����
��٤��������Ȥ�����Τ褦�ʶ������Ť��ͤ�����ʤ顢
����� 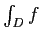 ��������롣
��������롣
���꤬�����Ĥ����롣
- ����������
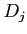 ������
������ 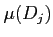 ��ǡ���������������������
����ˤϼ���
��ǡ���������������������
����ˤϼ��� 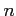 �ˤĤ��Ƶ�ǼŪ�˵�������
�ˤĤ��Ƶ�ǼŪ�˵�������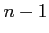 ��������ʬ��������뤫��
�⤷����
��������ʬ��������뤫��
�⤷���� 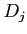 �Ȥ���ľ���ΤΤ褦�ʸ���Ū�ʤ�ΤΤߤ���ˡ�����롣
�Ȥ���ľ���ΤΤ褦�ʸ���Ū�ʤ�ΤΤߤ���ˡ�����롣
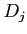 �Ȥ���ľ���ΤΤ褦�ʸ���Ū�ʤ�Τ�Ȥ���硢
�Ȥ���ľ���ΤΤ褦�ʸ���Ū�ʤ�Τ�Ȥ���硢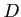 �Τ褦�ʤ�Τ�
�����ʤ�ʤ�����Ȥ����ʤ롣
����ˤϼ㴳�Ρ֤Ϥ߽Ф��פ⤷���ϡ�����ʬ�פ�����ơ�
���ȤǤ����δ�Ϳ����ʬ�������ʤ뤳�Ȥ���ˡ�����롣
�Τ褦�ʤ�Τ�
�����ʤ�ʤ�����Ȥ����ʤ롣
����ˤϼ㴳�Ρ֤Ϥ߽Ф��פ⤷���ϡ�����ʬ�פ�����ơ�
���ȤǤ����δ�Ϳ����ʬ�������ʤ뤳�Ȥ���ˡ�����롣
- ��ʬ��٤�������Ȥ����Ϥ�������������
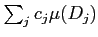 ��
�������ʤ���������������
��
�������ʤ��������������� 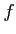 ���ɤΤ褦�ʴؿ����ˤ�ä��Ѥ�äƤ��롣
(����ѥ��Ƚ�����Ϣ³�ؿ��ʤ��
���ɤΤ褦�ʴؿ����ˤ�ä��Ѥ�äƤ��롣
(����ѥ��Ƚ�����Ϣ³�ؿ��ʤ�� 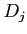 ��ǰ��Ͷ���Ǥ����������)
��ǰ��Ͷ���Ǥ����������)
- ���Τ褦����ʬ�Ϻ�ɸ�μ�����ˤ��ʤ���������? (��ľ���Ρפ�
����˺�ɸ�μ�����˰�¸���롣���ʤ����ľ���ΤϺ�ɸ�Ѵ�������̤Υ�Τˤʤä�
���ޤ���)
��ޥ���ʬ�Ϥ������������˲�����Ϳ���뤬����ʬ�Ȥϸ����ʤ���
Ű��Ū�˲�褹�뤿��ˤϥ�١�����ʬ�����᤹�롣
�����ϸ��äƤ⡢�֤ʤ�Ǥ⤫��Ǥ��١�����ʬ�פǤ������̣�����������줷��
����ʤΤǡ�����äȤ��餤�ϰ��äƤ�������
̿�� 10.1
��������γ�¬�٤�����ǡ�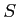 ��ʤ�����ľ���Τϸߤ��˸���ʤ�
��ΤΤߤ˸��ꤷ�Ƥ��̤Ϥ��ʤ��Ǥ��롣
��ʤ�����ľ���Τϸߤ��˸���ʤ�
��ΤΤߤ˸��ꤷ�Ƥ��̤Ϥ��ʤ��Ǥ��롣
���̿��ϥ�������ή�Ρ���ͭ�¤ζ��ľ���Τ�ʤ���פ���������
̿��ǡ���١���ή�Ρ��ֲĻ��Ĥ�ʤ������ˡ�ǤϤ�Ϥ�ʤꤿ���ʤ���
�� 10.2
- ���ľ���Τ�¬�ٳ���Ǥ��ꡢ
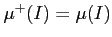 .
.
- ���̤�ͭ������
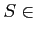
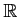
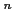 �ˤ������ơ�
�ˤ������ơ�
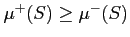 ���ʤꤿ�ġ�
���ʤꤿ�ġ�
��Τ��Ȥ����뤫�顢
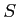 ¬�ٳ���ξ���
¬�ٳ���ξ��� 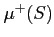 �Τ��Ȥ�ñ��
�Τ��Ȥ�ñ�� 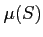 �ȽƤ⺹���٤��ʤ���
�ȽƤ⺹���٤��ʤ���
���� 10.1
ʿ�̻��ѷ�
����Ĺ������ʤ�äơ�
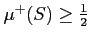
��������ʤ�����
�ռ��������ξ���
����9.1 �ε���ǤĤ��Τ褦�ʷ���Ԥ��ȡ�
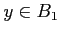 ��ߤ�뤴�Ȥˡ�
��ߤ�뤴�Ȥˡ�
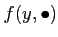 ���̾������Ǥ��뤳��
(�������ä�����9.3������������)�������롣
���̾������Ǥ��뤳��
(�������ä�����9.3������������)�������롣
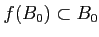 ��������٤�����������ϡ���������פȤ���
�Ĥ��Ƥ�������(��ݡ�������ǤϤʤ���))
��������٤�����������ϡ���������פȤ���
�Ĥ��Ƥ�������(��ݡ�������ǤϤʤ���))
�������μ�ĥ(3)�ˤ�ꡢ����9.3 �Ρֳ�����«�פϼ¤ϡְ��ͼ�«�פ�
���äƤ����������Ȥ�ʬ���롣Ϣ³�ؿ��ΰ��Ͷ˸¤�Ϣ³�Ǥ��뤫�顢
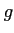 ��Ϣ³�ؿ��Ǥ��롣
��Ϣ³�ؿ��Ǥ��롣
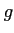 ������ˤ�ꡢ
������ˤ�ꡢ
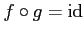 �Ǥ��뤳�Ȥ��ưפ�ʬ���롣���Ȥ�
�����Ǥ���褦��
�Ǥ��뤳�Ȥ��ưפ�ʬ���롣���Ȥ�
�����Ǥ���褦��



Next: About this document ...
2009-06-26
![]() ¿�ѿ��ؿ���(��ޥ�)��ʬ
¿�ѿ��ؿ���(��ޥ�)��ʬ
![]()
![]() ����ʬ����
����ʬ����
![]() ���������줿�¿��ͤ⤷���ϥ٥��ȥ��ʹؿ�
���������줿�¿��ͤ⤷���ϥ٥��ȥ��ʹؿ� ![]() ���Ф��ơ�
���Ф��ơ�
![]() ��
�� ![]() �����ʬ(����ʬ)�ϼ��Τ褦���������롣
�����ʬ(����ʬ)�ϼ��Τ褦���������롣
![]() ¬�ٳ���ξ���
¬�ٳ���ξ��� ![]() �Τ��Ȥ�ñ��
�Τ��Ȥ�ñ�� ![]() �ȽƤ⺹���٤��ʤ���
�ȽƤ⺹���٤��ʤ���
![]() ��ߤ�뤴�Ȥˡ�
��ߤ�뤴�Ȥˡ�
![]() ���̾������Ǥ��뤳��
(�������ä�����9.3������������)�������롣
���̾������Ǥ��뤳��
(�������ä�����9.3������������)�������롣
![]() ��������٤�����������ϡ���������פȤ���
�Ĥ��Ƥ�������(��ݡ�������ǤϤʤ���))
��������٤�����������ϡ���������פȤ���
�Ĥ��Ƥ�������(��ݡ�������ǤϤʤ���))