![]() пњљ’Љпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљ’Љпњљпњљпњљпњљпњљпњљпњљпњљпњљ
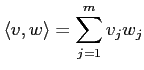
пњљпњљпњљпњљпњљпњљпњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљпњљл°£
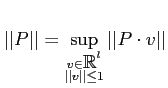
пњљпњљпњљпњљпњљпњљпњљпњљл°£
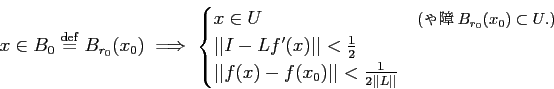
пњљпњљпњљ §к§њпњљƒ°пњљ
пњљпњљпњљпњљпњљпњљпњљпњљќЊпњљпњљпњљпњљќ•пњљпњљпњљѕ°пњљпњљ ≤пњљпњљпњљпњљпњљпњљпњљ(Newton Ћ°)пњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљпњљ![]() пњљќµ’єпњљпњљпњљќ§»§пњљпњљпњљпњљпњљ
пњљќµ’єпњљпњљпњљќ§»§пњљпњљпњљпњљпњљ
![]() пњљпњљпњљ÷§пњљпњљпњљпњљпњљпњљпњљпњљпњљ ђпњљпњљпњљпњљпњљпњљ ™пњљпњљ Newton Ћ°пњљ»§ѕ∞џ§ §л°£
пњљпњљпњљ÷§пњљпњљпњљпњљпњљпњљпњљпњљпњљ ђпњљпњљпњљпњљпњљпњљ ™пњљпњљ Newton Ћ°пњљ»§ѕ∞џ§ §л°£
пњљпњљпњљпњљ»°пњљ
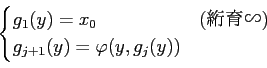
пњљпњљпњљпњљпњљ
пњљќ§»§пњљпњљпњљ
пњљ»§пњљпњљЋ°пњљ
пњљ’Љпњљпњљпњљпњљпњљпњљпњљпњљ«§ѕ°пњљпњљпњљпњљпњљпњљпњљпњљЌ∞пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљ §пњљпњљпњљпњљпњљпњљпњљ ![]() пњљ«§пњљ
пњљ«§пњљ ![]() пњљпњљпњљпњљ ђ
пњљпњљпњљпњљ ђ
![]() пњљпњљ
пњљƒµ’§«§пњљпњљл§≥пњљ»§пњљ≈ђпњљ—§ќ•Ё•пњљпњљпњљ»§«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ§и§¶пњљ єЌ§пњљпњљпњљпњљпњљпњљ—§пњљпњљ∆°пњљ
пњљпњљпњљпњљпњљпњљпњљЌ∞пњљќЉпњљпњљпњљпњљпњљпњљг§¶пњљпњљпњљЋ§в°Ґпњљ’іЎњпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ—§пњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљ«§пњљпњљпњљё§пњљпњљ єЌ§пњљпњљпњљпњљќ§яљс§§§∆§пњљпњљпњљпњљпњљпњљпњљ(пњљ№Їў§ѕЄпњљжЄ¶пњљпњљ)
пњљпњљ
пњљƒµ’§«§пњљпњљл§≥пњљ»§пњљ≈ђпњљ—§ќ•Ё•пњљпњљпњљ»§«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ§и§¶пњљ єЌ§пњљпњљпњљпњљпњљпњљ—§пњљпњљ∆°пњљ
пњљпњљпњљпњљпњљпњљпњљЌ∞пњљќЉпњљпњљпњљпњљпњљпњљг§¶пњљпњљпњљЋ§в°Ґпњљ’іЎњпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ—§пњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљ«§пњљпњљпњљё§пњљпњљ єЌ§пњљпњљпњљпњљќ§яљс§§§∆§пњљпњљпњљпњљпњљпњљпњљ(пњљ№Їў§ѕЄпњљжЄ¶пњљпњљ)
пњљпњљ
пњљпњљ¬Єпњљя§пњљпњљл°£ пњљпњљпњљ §пњљпњљпњљпњљ
пњљт§є§ў§∆§пњљ
пњљпњљпњљпњљЁ°пњљпњљпњљпњљпњљпњљпњљ
(пњљпњљпњљ¬°пњљпњљпњљпњљќє÷µпњљпњљќљпњљќїпњљпњљпњљё§«°пњљ)
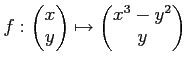
пњљ §пњљ(пњљпњљпњљ—њпњљпњљў•пњљпњљ»•пњљпњљпњљ)пњљЎњпњљпњљпњљ