![]() ¿�ѿ��ؿ��Υƥ��顼Ÿ��
¿�ѿ��ؿ��Υƥ��顼Ÿ��
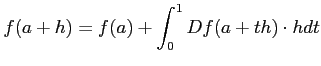
������Ω�ġ�
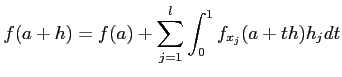
�����ξ����ˤ�
�ˤ���������ʬ��ʬ�ؤδ���������Ԥ����ɤ���
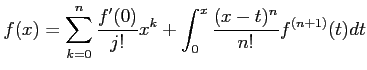
��μ����˻������Ƹ��ˤ��������Τ�ʤ��� ���Τ褦�ʺ�����
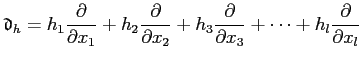
����ȡ���������μ��ϼ��Τ褦�ˤ���Ȥ��Ǥ��롣
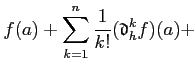 |
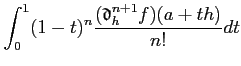 |
���ѿ��ξ��ˤĤ��ơ��ƥ��顼Ÿ�����ɤ��������˸����뤫�ˤĤ��Ƥ� ���ʽ��4.3.2�⻲�ȤΤ��ȡ�
����ݡ�������
(���¡����ιֵ��ν�λ���ޤǡ�)