![]() ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ËĪïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―Ņŋïŋ―ïŋ―Øŋïŋ―ïŋ―ÎĨÆĨïŋ―ïŋ―饞Åļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ËĪïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―Ņŋïŋ―ïŋ―Øŋïŋ―ïŋ―ÎĨÆĨïŋ―ïŋ―饞Åļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪĮĪÏĄïŋ―ïŋ―ÄĪïŋ―ïŋ―ÎĪčĪĶïŋ―ĘĪïŋ―ïŋ―ČĪōĪŋĪÓĪïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ëĄĢ
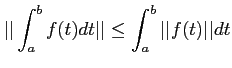
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĄïŋ―
ïŋ―č―ĩïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―5.3 ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪÃĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ηŨŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÜĪËĪĘĪëĄĢ ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―Îīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æ°ŨĪË―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Îūïŋ―įĄĢ
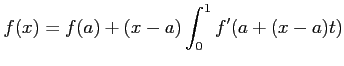
ïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Îūïŋ―įĄĢ
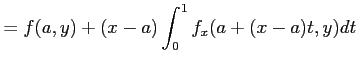 |
||
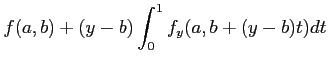 |
||
 |
 |
||
 |
||
 |
||
 |
||
 |
ïŋ―Ęūïŋ―ÏĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ÏĄÖžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņēïŋ―ïŋ―ōĩ―ŌĪïŋ―ïŋ―ïŋ―ŨĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―éĪŊïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÂĪÎēïŋ―ïŋ―ĮĄïŋ―ïŋ―ïŋ―ÏŦïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―Ëķïŋ―ÅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―Ãķïŋ―ïŋ―ïŋ―ïŋ―5.3 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ęĪ·ïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―
ïŋ―Ëķïŋ―ÅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―Ãķïŋ―ïŋ―ïŋ―ïŋ―5.3 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ęĪ·ïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―![]() ïŋ―ïŋ―Øŋïŋ―ïŋ―Ïžïŋ―Æ°ÅŠïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―Į―ïŋ―ĮĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―éĄĒïŋ―ÖĪÞĪÃĪïŋ―ïŋ―ïŋ―ïŋ―Ũķïŋ―ÅĪïŋ―ïŋ―ÛĪïŋ―ïŋ―ïŋ―ïŋ―ïĪŦïŋ―ïŋ―äĪđïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Øŋïŋ―ïŋ―Ïžïŋ―Æ°ÅŠïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―Į―ïŋ―ĮĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―éĄĒïŋ―ÖĪÞĪÃĪïŋ―ïŋ―ïŋ―ïŋ―Ũķïŋ―ÅĪïŋ―ïŋ―ÛĪïŋ―ïŋ―ïŋ―ïŋ―ïĪŦïŋ―ïŋ―äĪđïŋ―ïŋ―ïŋ―ïŋ―
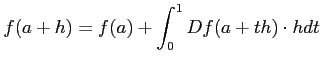
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĄïŋ―
ïŋ―ÔđâģŽïŋ―ïŋ―ĘŽïŋ―ïŋ―
ïŋ―ÏĄïŋ―
ïŋ―Č―ņĪĪĪïŋ―,
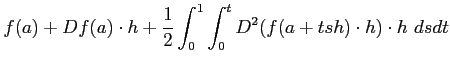 |
||
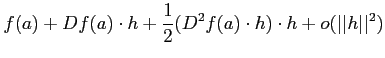 |
ïŋ―ïŋ―ĘŽïŋ―ïŋ―Æąïŋ―ÍĪËđâģŽïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―Æĩïŋ―ïŋ―ŌĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĄïŋ―
(2)ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Îūïŋ―įĪŽïŋ―Üžïŋ―ÅŠïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―Æŧïŋ―ÚĪïŋ―ïŋ―ïŋ―ĘŽÉ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪËĪĘĪëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ÝĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ÂĄïŋ―ïŋ―ïŋ―ïŋ―ÎđÖĩïŋ―ïŋ―Î―ïŋ―Îŧïŋ―ïŋ―ïŋ―ÞĪĮĄïŋ―)
ïŋ―ïŋ―
ïŋ―ĘĪïŋ―Âŋïŋ―