��ϳ� IA No.5��

(��)��ʬ��ְ켡��פȤ��ƤȤ館��ȡ� ��ؿ��ʬ��Ѥ䤵��

�� 5.1 $\mbox{${\mathbb{R}}$}$ �γ�� $\mbox{${\mathbb{R}}$}$ �ؤμ�� ȡ� ��ʬ��Ȥ�� ޤ೫�� $\mbox{${\mathbb{R}}$}$ �ؤμ�� Ϳ��Ƥ��Ȥ��롣 ��ΤȤ��⤷ �� $a\in U$ ��ʬ��ǽ�ǡ� �ʤ�� ʬ��ǽ�ʤ�С� ��ؿ� $g\circ f$ �� ʬ��ǽ�Ǥ��äơ�

$\displaystyle D(g\circ f)_a= (D g)_{f(a)}\cdot (D f) _a$

(`` $\cdot$ " �Ϲ��)��Ω�ġ�

��.

, $(D g)_{b}=M$ �Ƚ񤯤ȡ�

	$% latex2html id marker 1076 $\displaystyle f(a+v)=f(a)+L v + o(\vert\vert v\vert\vert)\quad (=b+L v +o(\vert\vert v\vert\vert))$$
	$\displaystyle g(b+w)=g(b)+M w + o(\vert\vert w\vert\vert).$

��Τ��Ȥ��顢

	$\displaystyle g(f(a+v))=g(b+ L v +o(\vert\vert v\vert\vert))$
$\displaystyle =$	$\displaystyle g(b)+ M\cdot (L v + o(\vert\vert v\vert\vert)) + o(\vert\vert L v + o(\vert\vert v\vert\vert)\vert\vert)$
$\displaystyle =$	$\displaystyle g(f(a))+ M\cdot L v + o(\vert\vert v\vert\vert))$

��狼�롣 $% latex2html id marker 1070 $ \qedsymbol$$

��ʬ�ι��ʬ��ʬ��Ǥ��ä��Ȥ�פ��Ф��ȡ� ��ηϤ��롣

�� 5.2 (``��4.6, ��4.7'') ��ξ��β��ǡ� $\mbox{${\mathbb{R}}$}$ $\mbox{${\mathbb{R}}$}$ $\mbox{${\mathbb{R}}$}$ �κ�ɸ�Ϥ� ��줾�� $(x_1,x_2,\dots,x_l)$ , $(y_1,y_2,\dots,y_m)$ , $(z_1,z_2,\dots,z_n)$ �Ȥ��ơ� ��ʬ��ɽ��ȡ�

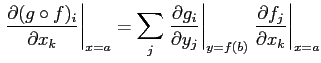
$\displaystyle \left.\frac{\partial (g\circ f)_i} {\partial x_k}\right \vert _{x... ... \vert _{y=f(b)} \left. \frac{\partial f_ j} {\partial x_k}\right\vert _{x=a}$

�� 5.1

	$\displaystyle f:$ $\displaystyle \mbox{${\mathbb{R}}$}$ $\displaystyle ^2 \ni (u,v) \mapsto (u, u+v^3) \in$ $\displaystyle \mbox{${\mathbb{R}}$}$ $\displaystyle ^2$
	$\displaystyle g:$ $\displaystyle \mbox{${\mathbb{R}}$}$ $\displaystyle ^2 \ni (x,y) \mapsto x^3 y \in$ $\displaystyle \mbox{${\mathbb{R}}$}$

��ͤ��ȡ�

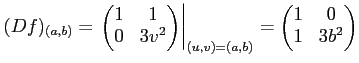	$\displaystyle (Df)_{(a,b)}= \left . \begin{pmatrix}1 &1 0 & 3 v^2 \end{pmatrix} \right \vert _{(u,v)=(a,b)} = \begin{pmatrix}1 &0 1 & 3 b^2 \end{pmatrix}$
	$\displaystyle (Dg)_{(x_0,y_0)}= \left . \begin{pmatrix}3 x^2 y & x^3 \end{pmatr... ...ight \vert _{(x,y)=(x_0,y_0)} =\begin{pmatrix}3 x_0^2 y_0 & x_0^3 \end{pmatrix}$

�Ȥ��ˡ�

$\displaystyle (Dg)_{f(a,b)}= =\begin{pmatrix}3 a^2 (a+b^3) & a^3 \end{pmatrix}$

�Ȥ��ˡ�

¾��ǡ�

$\displaystyle (g\circ f)(u,v)=u^3 (u+v^3)$

�Ǥ��뤫�顢

$\displaystyle (D(g\circ f))_{(a,b)}= \begin{pmatrix} 4 a^3 +3 a^3 b^3& 3 a^3 b^2 \end{pmatrix}$

�Ǥ��äơ��ñ�ʹ��󻻤ˤ�ꡢ��ξ��ºݤ��Ȥ� �Τ��롣

�ѿ��ο�

��Ѥ��ơ��ηϤ򤤤��񤭴��Ƥߤ��ɤ�� ``Ϣ��Χ''�δ��Ϥ��Ϣ��Χ�ϡ��ѿ��Ѵ��ͤ��ݤ��ä˽��פˤʤ롣

�� 5.1 $\mbox{${\mathbb{R}}$}$

�γ��

�� $\mbox{${\mathbb{R}}$}$

�ؤμ��

�� ʬ��

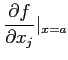
$\displaystyle \frac{\partial f}{ \partial x_j}\vert _{x=a}$

��

�δؿ��Ȥߤ��Τ�

��

�Ǥ� ��Ƴ�ؿ��Ȥ�֡�

��Ǥϡ�

�Ȥ��Ƥϥ٥��ȥ��ͤ��Ƶ��Ҥ�� Ǥ�

��٥��ȥ�Τޤޤǰ��äƤ��ɤ��ΤǤ��뤬�� ʬ�ǽ񤤤Ƥ��Ȥˤ��롣

�� 5.2 $\mbox{${\mathbb{R}}$}$

�γ��

�� $\mbox{${\mathbb{R}}$}$

�ؤμ��

��

�ˤ��

-��Ǥ��Ȥ�,

��Ƥ��ʬ��Ƥ��Ƴ�ؿ�

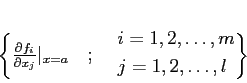
$\begin{equation*} % latex2html id marker 1177\left\{ \frac{\partial f_i}{ \par... ...ligned} &i=1,2,\dots,m\\ & j=1,2,\dots,l \end{aligned}\right \} \end{equation*}$

��¸�ߤ��ơ�� $a\in U$ �ˤĤ��Ϣ³�Ǥ��Ȥ��ˤ��

��ϡ��Τ��䤹��ʬ��Ѥ��Ƥ��Τ� ��Фä��״��Ǥ��롣

�� 5.3 $\mbox{${\mathbb{R}}$}$ �γ�� $\mbox{${\mathbb{R}}$}$ �ؤμ�� ˤĤ��ơ� ��Ʊ�ͤǤ��롣

�Ͼ��ΰ�̣�� Ǥ��롣
�� γ��ʬ��ǽ�ǡ� ��ʬ $Df\vert _{x=a}$ �� ˤĤ��( �� $M_{m,l}($ $\mbox{${\mathbb{R}}$}$ -�ʹؿ��Ȥ��) Ϣ³�Ǥ��롣

�� 5.1 ��β��β��ǡ� $x\in U$ �� $B_r(x)\subset U$ �Ȥ��롣 �� ʤ�С�

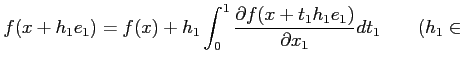
$% latex2html id marker 1229 $\displaystyle f(x+h_1 e_1 )=f(x)+h_1 \int_0^1 \frac{\partial f(x+ t_1 h_1 e_1)}{\partial x_1} d t_1 \qquad ( h_1\in$$ $\displaystyle \mbox{${\mathbb{R}}$}$ $\displaystyle , \vert h_1\vert<r )$

��ʤꤿ�ġ��ˡ� $e_1=(1,0,0,\dots,0)$ �ϴ��ܥ٥��ȥ�Ǥ��롣 (Ʊ�ͤ�ɽ��¾�μ��ˤĤ��Ƥ��Ω�ġ�)

�� 5.4 $\mbox{${\mathbb{R}}$}$ �� ѥ��Ƚ�� $\mbox{${\mathbb{R}}$}$ -��Ϣ³�ؿ� �ϰ��Ϣ³�Ǥ��롣 ��ʤ��

$\displaystyle \forall \epsilon >0 \exists \delta >0 \forall x,\forall y \in K (d(x,y) <\delta \implies d(f(x),f(y))<\epsilon)$

���ϳ� IA No.5����

��ϳ� IA No.5��