![]() ������ʬ������ʬ��
������ʬ������ʬ��
¿�ѿ��ؿ����顢��¾���ѿ���ߤ�ư�Ĥ������ѿ������ܤ���פ��Ȥˤ�ꡢ ���ѿ��ؿ������뤳�Ȥ��Ǥ��롣���ΰ�̣��¿�ѿ��ؿ��Ϥ�����ʬ�ˤĤ��ơ� �������٤��ΤäƤ��뤳�Ȥˤʤ롣
��ͤ����Ȥ��ˡ����줬
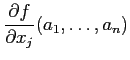 �Ȥ�
�Ȥ� 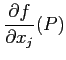 �Ȥ�
�Ȥ� �ʤɤȽ�
����ʬ�����ϡ��ְ�Ĥ��ѿ�����������ư�����Ȥɤ��ʤ뤫�פˤĤ��Ƹ�äƤ���� ���Ǥ��롣�ǤϤ����������ѿ��줾�쾯������ư�����Ȥɤ��ʤ��������?
�Ƚơ�
¿�ѿ�����ʬ�ϥ٥��ȥ�ȹ���ε�ˡ��Ȥä��ۤ������ä��ꤹ�롣
�ʲ��Ǥ�
![]()
![]() ��
��
![]()
![]() ���
(���̤��Թ�Dz��˽Ƥ�����⤢�뤬������Ū�ˤ�����)
�ֽĥ٥��ȥ�פ��Ȼפä�ĺ��������
���
(���̤��Թ�Dz��˽Ƥ�����⤢�뤬������Ū�ˤ�����)
�ֽĥ٥��ȥ�פ��Ȼפä�ĺ��������
������Ω�ĤȤ��ˤ�����
����ʬ�ϡ�![]() �ΰ켡�����Ϳ���롣����ʬ��
�ΰ켡�����Ϳ���롣����ʬ�� ![]() ������������
������������ ![]() �˶�Ť��Ȥ���
�˶�Ť��Ȥ��� ![]() �ε�ư��Ϳ���Ƥ��뤫�顢����ʬ��ʬ���äƤ����
����ʬ�ϼ�ưŪ������ʬ������Ǥ��뤳�Ȥˤʤ롣
�ε�ư��Ϳ���Ƥ��뤫�顢����ʬ��ʬ���äƤ����
����ʬ�ϼ�ưŪ������ʬ������Ǥ��뤳�Ȥˤʤ롣
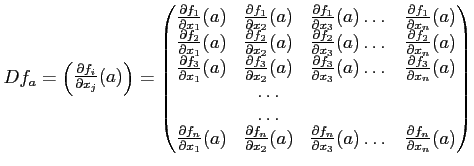
���Ѿ�ϡ�����ʬ�Υǡ������Ѥ�������ʬ�ι�����ʬ������Ȥ������� ����������Ȥ��뤳�Ȥ�¿����
����ݡ�������
(���¡����ιֵ��ν�λ���ޤǡ�)