![]() ïŋ―ïŋ―Âŋïŋ―Ņŋïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ČķËļïŋ―(2)ïŋ―ïŋ―
ïŋ―Öžïŋ―ïŋ―ïŋ―ïŋ―ŨĪČĄÖīØŋïŋ―ïŋ―ŨĪïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ĖĢïŋ―Îļïŋ―ïŋ―ÕĪĮĪÏĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―ïŋ―ËĨåĨĒïŋ―óĨđĪČĪïŋ―ïŋ―ÆĪïŋ―
ïŋ―ÖīØŋïŋ―ïŋ―ŨĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Í―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―Æŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―Âŋïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ïŋ―ĘĄÖīØŋïŋ―ïŋ―ŨĪËļÂĪéĪšïŋ―ïŋ―ÃĪČ°ïŋ―ïŋ―ĖĪÎĄÖžïŋ―ïŋ―ïŋ―ïŋ―ŨĪïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Ëĩïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―ïŋ―ÜĪïŋ―ïŋ―ïŋ―ïŋ―Ï°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ųķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―Âŋïŋ―Ņŋïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ČķËļïŋ―(2)ïŋ―ïŋ―
ïŋ―Öžïŋ―ïŋ―ïŋ―ïŋ―ŨĪČĄÖīØŋïŋ―ïŋ―ŨĪïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ĖĢïŋ―Îļïŋ―ïŋ―ÕĪĮĪÏĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―ïŋ―ËĨåĨĒïŋ―óĨđĪČĪïŋ―ïŋ―ÆĪïŋ―
ïŋ―ÖīØŋïŋ―ïŋ―ŨĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Í―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―Æŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―Âŋïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ïŋ―ĘĄÖīØŋïŋ―ïŋ―ŨĪËļÂĪéĪšïŋ―ïŋ―ÃĪČ°ïŋ―ïŋ―ĖĪÎĄÖžïŋ―ïŋ―ïŋ―ïŋ―ŨĪïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Ëĩïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―ïŋ―ÜĪïŋ―ïŋ―ïŋ―ïŋ―Ï°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ųķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―Ëļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ÎĪÉĪïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ÏĒÂģïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ÎĪÉĪïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ÏĒÂģïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―![]() ïŋ―ïŋ―ÏĒÂģïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ÏĒÂģïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―šÝĪÎīØŋïŋ―ïŋ―ïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ĘīØŋïŋ―ïŋ―ïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪßđïŋ―ïĪŧïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ĘīØŋïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ÏĪČĪĘĪïŋ―ČĄïŋ― ïŋ―ïŋ―ïŋ―ïŋ―Ï·ïŋ―Éūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪËĪĘĪëĄĢ
ÏĒÂģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪßđïŋ―ïĪŧïŋ―Æŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪŋïŋ―ïŋ―ËĪÏĄïŋ― ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÎĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ęžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―Þžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍąÆĪĘĪïŋ―) ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ÐĪĘĪïŋ―ĘĪïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ųžïŋ―ÖĪËĪĘĪÃĪÆĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―Ξïŋ―ïŋ―ĘĪïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČūÞïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ÎĪĮĄïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ČĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―
ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() .
.
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪČĪïŋ―ïŋ―ïŋ―
ïŋ―Č―ņĪĪĪÆĄïŋ―
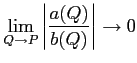
ïŋ―ïŋ―Æąïŋ―ÍĪĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Îĩïŋ―ËĄïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ČĄïŋ―![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ïŋ―ÏĒÂģïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪÏĄïŋ―
ïŋ―ïŋ―ÏĒÂģïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪÏĄïŋ―
ïŋ―ïŋ―Æąïŋ―ÍĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ÝĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ÂĄïŋ―ïŋ―ïŋ―ïŋ―ÎđÖĩïŋ―ïŋ―Î―ïŋ―Îŧïŋ―ïŋ―ïŋ―ÞĪĮĄïŋ―)