ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ― ïŋ―Ëļïŋ―
ïŋ―ïŋ―.ïŋ―ÍĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
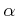 ïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ÎĪßĪĮĪčĪĪïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ÎĪßĪĮĪčĪĪïŋ―ïŋ―)
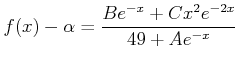
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―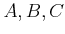 ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- ÅŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îŋïŋ―
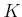 ïŋ―ïŋ―ČĪïŋ―ČĄïŋ―
ïŋ―ïŋ―ČĪïŋ―ČĄïŋ―
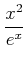 ïŋ―ïŋ―
ïŋ―ïŋ― 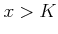 ïŋ―ïŋ―ïŋ―Ï°ÏĪïŋ―Íïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ĘŽïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÏĄïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Ï°ÏĪïŋ―Íïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ĘŽïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÏĄïŋ―
ïŋ―ïŋ―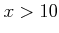 ïŋ―ĘĪïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―
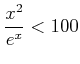 ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪßĪïŋ―ïŋ―ïŋ―ïŋ―ÆēōĪĪĪÆĪïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―)
ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪßĪïŋ―ïŋ―ïŋ―ïŋ―ÆēōĪĪĪÆĪïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―)
- ïŋ―ïŋ―ïŋ―ΞÂŋïŋ―
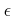 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
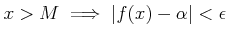
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―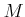 ïŋ―ïŋ―ïŋ―Äĩïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―Üūïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―Íģïŋ―ōĪĪïŋ―ïŋ―ïŋ―Č―ņĪŊĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ)
ïŋ―ïŋ―ïŋ―Äĩïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―Üūïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―Íģïŋ―ōĪĪïŋ―ïŋ―ïŋ―Č―ņĪŊĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ)
 .
.
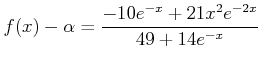
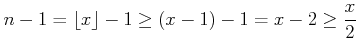
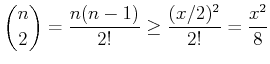
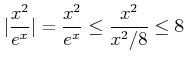
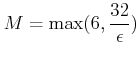
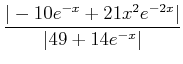
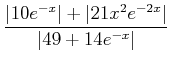 (ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)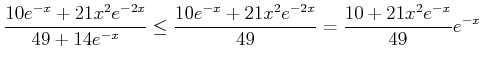
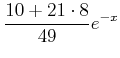 ((3)ïŋ―ËĪïŋ―ïŋ―)
((3)ïŋ―ËĪïŋ―ïŋ―)