![]()
����ϡ��������ΰ�̣�⤳��ơ���ݡ���12 �β�����Ҥ٤�ȤȤ�ˡ� ������ζ˸¤ΰ����ˤĤ��ƾ��������뤳�Ȥˤ��롣
��ݡ���12 �ϡ�
![]() �ΤȤ�������Ǥ��뤬��
�����
�ΤȤ�������Ǥ��뤬��
����� ![]() �ζ˸¤˺�꤫��������С��ѿ����Ѵ����Ƥ��Ȥ���
�ζ˸¤˺�꤫��������С��ѿ����Ѵ����Ƥ��Ȥ���
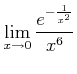
����������ͤ�����ɤ���
��äȰ��̤ˡ�
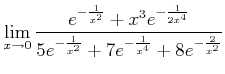
�ʤɤζ˸¤η��⡢�ɤιब�礭���ʤ뤫�������Ĥ��Ƥ���С� ���ѳڤ˷��Ǥ��롣
(����ϥ�ݡ��ȤϤ���ޤ���)
�轵�ϻ�Ǥ���
��������:¾�οͤμ���ˤʤ�ʤ���Ρ��̿���ǽ������ʤ���Τʤ�С� ���Ǥ�ġ�
��ˤǤ���������:
����ζ˸¤Ϥ��������������(����:
![]() .)
.)
��
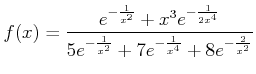
�Ȥ������Ȥ���
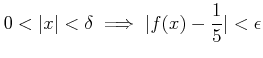
��ߤ����褦�ˤ���ˤϡ�
�����¤�����ݡ��Ȥϡ��������������������ͳ���ʤ��¤� �������ޤ���ΤǤ������餺��λ��������������
����12.1 ������
�����ˤ��Ĥ����ˡ�������������Ƥ�������
�¿� ![]() �ˤ������ơ�
�ˤ������ơ�![]() ����礭��������¸�ߤ��롣
(���륭��ǥ��θ�����)���ΰ�Ĥ�
����礭��������¸�ߤ��롣
(���륭��ǥ��θ�����)���ΰ�Ĥ� ![]() �Ȥ��褦��
�ޤ���
�Ȥ��褦��
�ޤ���![]() �ʲ���������¸�ߤ��뤳�Ȥ�(
�ʲ���������¸�ߤ��뤳�Ȥ�(![]() ���Ф��ƥ��륭��ǥ��θ���
��Ŭ�Ѥ��뤳�Ȥˤ��)ʬ���롣���ΰ�Ĥ�
���Ф��ƥ��륭��ǥ��θ���
��Ŭ�Ѥ��뤳�Ȥˤ��)ʬ���롣���ΰ�Ĥ� ![]() �Ȥ��褦��
����ȡ�
�Ȥ��褦��
����ȡ�![]() �ʲ��������Τ���
�ʲ��������Τ��� ![]() �ʾ�Τ�Τ�
�ʾ�Τ�Τ�
�Ȥ���ͭ�¸Ĥ������Υꥹ�ȤΤʤ��˴ޤޤ�Ƥ��ꡢ�Ȥ���
�Ƚ�����������С�
| (��) |
������Ϥ�褦���ޤ���
�ˤ�ꡢ
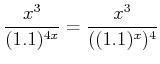 |
||
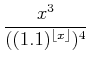 |
||
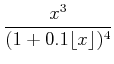 (�������) (�������) |
||
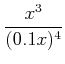 (�� ��) (�� ��) |
||
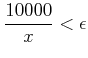 |
�����ϰϤ� ![]() ���Ф��ƤϤ������
���Ф��ƤϤ������
![]() �Ǥ��뤫�顢
�Ǥ��뤫�顢
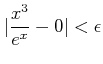
���ʤꤿ�Ĥ��Ȥ�ʬ���ä���
���� ������������ζ˸¤�����Ǥ��롣
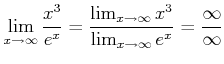
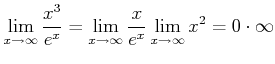
�ʤɤȤ�äƤ⡢�˸¤ϵ�ޤ�ʤ��� ��
�Ǥ�������ζ˸¤ϤɤΤ褦�˰������ɤ����ȸ����С���������Ǹ����� ![]() ��
�� ![]() �Ȥ��礭���ʤ꤫���ζ�����ѻ����뤳�Ȥˤʤ롣
�ֵ��Ǥ⾯���Ҥ٤��褦�ˡ����ζ���ϥϥå���֥����פ��Ĥ��Ƥ��ơ�
���ʤ깵���ܤ˸��Ѥ�äƤ�
�Ȥ��礭���ʤ꤫���ζ�����ѻ����뤳�Ȥˤʤ롣
�ֵ��Ǥ⾯���Ҥ٤��褦�ˡ����ζ���ϥϥå���֥����פ��Ĥ��Ƥ��ơ�
���ʤ깵���ܤ˸��Ѥ�äƤ� ![]() ���������롣�嵭�����Ϥ��Τ褦�ʸ��Ѥ���
����ˡ�Ǥ��롣
���������롣�嵭�����Ϥ��Τ褦�ʸ��Ѥ���
����ˡ�Ǥ��롣
���������һؿ��������Ǥʤ����ˤ��Ѥ��Ƥ��������¿���ä����� ��̩�ˤ��ֵܹ��Ǥ϶һؿ������������ξ�礷�����äƤ��ʤ��� �������äƾ嵭�����Τ褦�˾������פ�ɬ�פǤ��롣