![]()
ïŋ―ïŋ―
![]()
ïŋ―ïŋ―ïŋ― 5.5 ïŋ―ïŋ― ![]() ïŋ―ïŋ―ŨĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ŨĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
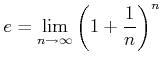
ïŋ―ÕīØŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ęĄĒ![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ïŋ―ÏĒÂģïŋ―Øŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―
ïŋ―ïĪŦïŋ―ëĄĢ
ïŋ―ïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ïŋ―ÏĒÂģïŋ―Øŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―
ïŋ―ïĪŦïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ØĪĮĪïŋ―ïŋ―ĮĪïŋ―ĘĪïŋ―ïŋ―ÂĪïŋ―ïŋ―Ðŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ― ![]() ïŋ―ïŋ―ČĪęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ðŋïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ĖĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ČĪęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ðŋïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ĖĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―Îĩïŋ―Æ°ïŋ―ōĩ―ŌĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Îĩïŋ―Æ°ïŋ―ōĩ―ŌĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ÎĪČĪïŋ―ïŋ―Îĩïŋ―Æ°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÎĪČĪïŋ―ïŋ―Îĩïŋ―Æ°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
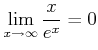
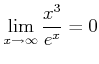
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ(ïŋ―ïŋ―ïŋ―ÎđÖĩïŋ―ïŋ―ĮĪïŋ―ïŋ―ÞĪÞĪĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÉĪïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ÆĪïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―10.2 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]()
![]()
![]() ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ÏĒÂģïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ĮĪïŋ―ÕĪïŋ―
ïŋ―ïŋ―ÏĒÂģïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ĮĪïŋ―ÕĪïŋ―
![]() ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
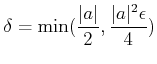
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ĘĪïŋ―ĮĪïŋ―ÕĪïŋ―
ïŋ―ĘĪïŋ―ĮĪïŋ―ÕĪïŋ― ![]() ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
![]() ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĪïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ËĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĪïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ËĄïŋ―![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĄïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĄïŋ―![]() ïŋ―ĮĪïŋ―ïŋ―ęĄĒ
Âūïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ęĄĒ
Âūïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―ïŋ―éĄĒ
ïŋ―ïŋ―ïŋ―éĄĒ
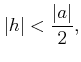 ïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ― |
(*) | |
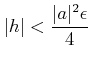 |
(**) |
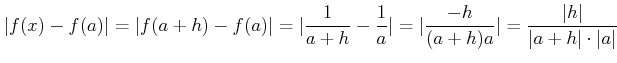 |
(A) |
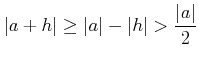
ïŋ―ĮĪïŋ―ïŋ―ÃĪÆĄïŋ― ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îŋïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÆĪÏĄïŋ―ĘŽïŋ―ėĪŽïŋ―įĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ÛĪÉĪïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―éĄĒ
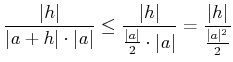 |
(B) |
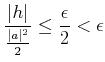 |
(C) |
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
(A),(B),(C)ïŋ―ïŋ―ÄĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïĪŧïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―
(ĮĪïŋ―ÕĪïŋ―
![]() ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―![]() ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ĘĪïŋ―ĮĪïŋ―ÕĪïŋ―
ïŋ―ĘĪïŋ―ĮĪïŋ―ÕĪïŋ― ![]() ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïĪŦïŋ―ÃĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Îēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―Öĩïŋ―ïŋ―Į―ŌĪŲĪïŋ―ïŋ―ïŋ―ïŋ―
| (ïŋ―ïŋ―) |
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ČĪïŋ―ÅŽïŋ―ïŋ―ïŋ―Ë°ÜđāĪđïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÕĄïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ĮīÖ°ãĪĻïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪŦĪĘĪïŋ―ïŋ―čĪĶïŋ―ËĄïŋ―ïŋ―ČĪïŋ―ïŋ―ËŧÏĪïŋ―ÎīÖĪïŋ― ïŋ―ïŋ―ïŋ―ÜĪÎŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―)ïŋ―ōĪ·ĪÃĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪÏĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ÍĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―