


Next: About this document ...
��ʬ��ʬ�س���AI���� No.11

��� 11.1 (``1.3.6'')
�¿��Τ�����
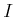
��������줿�ؿ�
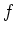
������ñĴ���ôؿ��Ǥ���Ȥϡ�
��ߤ����Ȥ��ˤ�����
���� 11.2 (``���ʽ�����1.16'')
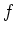
���Ķ��
![$ [a,b]$](img5.png)
��ζ���ñĴ���ä�Ϣ³�ؿ��Ǥ���С�
�εմؿ�
��¸�ߤ��롣
����ˡ�����
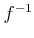
��Ϣ³�ǡ����Ķ���ñĴ���äǤ��롣
�� 11.3
��������
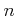
���Ф��ơ�
0
�ʾ�μ¿��������Ȥ���ؿ�
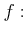
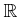
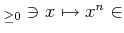
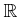
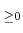
��Ϣ³�Ǥ��ꡢ����ñĴ���äǤ��롣���δؿ������ͤǤ⤢�뤫�顢
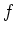
�ϵռ�������ġ����δؿ���
�Ƚ�
�Ĥޤ�
![% latex2html id marker 1021
$ y=\sqrt[n]{x}$](img15.png)
��
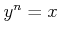
��������ͣ������μ¿��Ǥ��롣
̿�� 11.4
Ǥ�դ����μ¿�
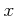
���Ф��ơ�
���ʤꤿ�ġ�
Proof.
![% latex2html id marker 1037
$ y=\sqrt[n]{x}$](img20.png)
�Ȥ����ȡ�����ˤ�ꡢ
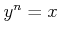
.
�椨�ˡ�
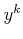
��
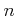
�褷��
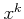
�ˤʤ�¿��Ǥ��롣
���Τ褦�ʼ¿���ͣ��ġ����ʤ��
![% latex2html id marker 1049
$ \sqrt[n]{x^k}$](img24.png)
�����ʤ��ΤǤ��뤫�顢
ξ�Ԥ���������
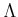
Ʊ�ͤˤ��ơ����Τ��Ȥ�ʬ���롣
̿�� 11.5
��������
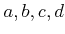
��
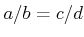
���������С�Ǥ�դμ¿�
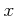
�ˤ������ơ�
���ʤꤿ�ġ�
����̿�꤬�ʤꤿ�ĤΤǡ�
![% latex2html id marker 1064
$ \sqrt[b]{x^a}$](img28.png) �Τ��Ȥ�
�Τ��Ȥ�
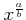 ��
�Ƥ����ζ��줬�ʤ���
��
�Ƥ����ζ��줬�ʤ���
�� 11.6
������Ǥϡ���ǽ������Ѵؿ����μ���
���ΤǤ���Ȥ��롣
-
![$ [-\frac{\pi}{2},\frac{\pi}{2}] \ni x\mapsto \sin(x) \in [-1,1]$](img30.png) �϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
�϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
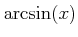 �Ƚ�
�Ƚ�
-
![$ [0,\pi] \ni x\mapsto \cos(x) \in [-1,1]$](img32.png) �϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
�϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
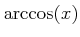 �Ƚ�
�Ƚ�
-
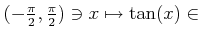
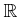 �϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
�϶���ñĴ����Ϣ³�ؿ��Ǥ��롣���εմؿ��Τ��Ȥ�
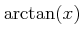 �Ƚ�
�Ƚ�
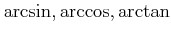 �Ϥ��줾��
�Ϥ��줾��
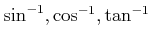 �ʤɤȽ��Ȥ⤢�롣
�ʤɤȽ��Ȥ⤢�롣
���� 11.1
��������
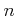
�ˤ�������
![% latex2html id marker 1097
$ a_n=\sqrt[n]{2}$](img38.png)
�Ȥ�����
���ΤȤ�������
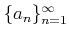
��
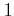
�˼�«���뤳�Ȥ�
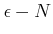
ˡ���Ѥ��ƾ������ʤ�����
���� 11.2
���Τ��Ȥ��ʤ�����
(��ݡ������꤬����ʾ夢����Ϥɤ��餫������Ф褤��)
����9.1 ������
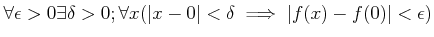 |
(��) |
�����ꡢ���ʤ��
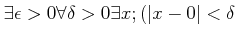 and and 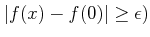 |
(��) |
�����ɤ���
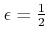 �����롣
�ɤ��
�����롣
�ɤ�� 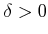 ��ȤäƤ��Ƥ⡢
��ȤäƤ��Ƥ⡢
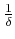 ����礭������
����礭������ 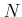 ��¸�ߤ���
(���륭��ǥ��θ���)��
��¸�ߤ���
(���륭��ǥ��θ���)��
���� 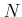 �ˤ�������
�ˤ�������
�Ȥ����С�
�ʤΤˡ�
�ǡ��Ȥ���
�Ǥ��롣
��ξ��������ɽ�����뤳�Ȥ��Ǥ��롣
(��) �ˤ����ơ�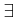 ����ΤĤ��Ƥ����ѿ����̣��¦�פ��ѿ���
����ΤĤ��Ƥ����ѿ����̣��¦�פ��ѿ���
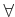 ����ΤĤ��Ƥ���ۤ����Ũ¦�פ��ѿ��ȸ��뤳�Ȥˤ��褦��
̣��¦���ѿ��Ϥ�����Ƿ������ɤ�(����٤��Ǥ���)�Τˤ�������
Ũ¦���ѿ��Ϥ����餫����뤳�ȤϤǤ��ʤ���
����
����ΤĤ��Ƥ���ۤ����Ũ¦�פ��ѿ��ȸ��뤳�Ȥˤ��褦��
̣��¦���ѿ��Ϥ�����Ƿ������ɤ�(����٤��Ǥ���)�Τˤ�������
Ũ¦���ѿ��Ϥ����餫����뤳�ȤϤǤ��ʤ���
����
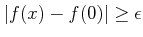 ���ǽ�Ū����Ω���뤳�Ȥ��̣���ξ�����
�ȸƤ٤С�
��ξ�����̣����ɬ���Ǥ���(�褦��̣������ά������)���Ȥ�ɽ���Ƥ��롣
���ǽ�Ū����Ω���뤳�Ȥ��̣���ξ�����
�ȸƤ٤С�
��ξ�����̣����ɬ���Ǥ���(�褦��̣������ά������)���Ȥ�ɽ���Ƥ��롣
����
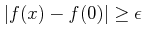 .
.
������� 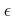 �Ȥ���
�Ȥ���
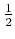 ���������Ф���Ũ¦
���������Ф���Ũ¦
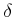 �ϰճ��ʰ�ꡣ������錄����
�ϰճ��ʰ�ꡣ������錄���� 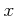 �Ť����ӡ�
�����˷�ӤĤ����ΤǤ��ä���
�Ť����ӡ�
�����˷�ӤĤ����ΤǤ��ä���
|
(��)�ι�������촹����(Ũ¦����į�)��Τ�(��)�Ǥ��롣
�㤨��
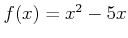 ��
�� 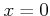 �ˤ�����Ϣ³���᤹�Τϡ��ʲ��Τ褦�ʥ�������ά��ͤ��Ƥ���Τ�Ʊ���Ǥ��롣
�ˤ�����Ϣ³���᤹�Τϡ��ʲ��Τ褦�ʥ�������ά��ͤ��Ƥ���Τ�Ʊ���Ǥ��롣
����
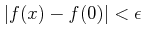 .
.
Ũ¦ 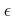 �ϰճ��ʰ�ꡣ�Ф��뤳����Ϥ����
���Ť�
�ϰճ��ʰ�ꡣ�Ф��뤳����Ϥ����
���Ť� 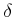 �������줬ɬ���ΰ��Ǥ��ä���
�ʲ���Ũ¦
�������줬ɬ���ΰ��Ǥ��ä���
�ʲ���Ũ¦ 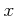 �������Ȼ�ߤ�ȿ�⤹��⡢��κפ�Ǥ��ä���
�������Ȼ�ߤ�ȿ�⤹��⡢��κפ�Ǥ��ä���
|
��Ƥ�ʬ����褦�ˡ�(��),(��)�Ϥ��줾�켡�Τ褦�˸��������Ƥ��ɤ���
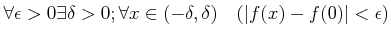 |
(��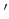 )
) |
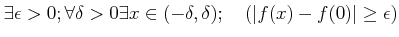 |
(��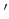 )
) |



Next: About this document ...
2009-07-07
![]()
![]() �����롣
�ɤ��
�����롣
�ɤ�� ![]() ��ȤäƤ��Ƥ⡢
��ȤäƤ��Ƥ⡢
![]() ����礭������
����礭������ ![]() ��¸�ߤ���
(���륭��ǥ��θ���)��
��¸�ߤ���
(���륭��ǥ��θ���)��
![]() �ˤ�������
�ˤ�������
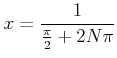
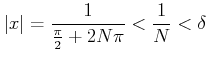
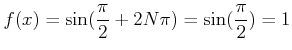
![]() ����ΤĤ��Ƥ����ѿ����̣��¦�פ��ѿ���
����ΤĤ��Ƥ����ѿ����̣��¦�פ��ѿ���
![]() ����ΤĤ��Ƥ���ۤ����Ũ¦�פ��ѿ��ȸ��뤳�Ȥˤ��褦��
̣��¦���ѿ��Ϥ�����Ƿ������ɤ�(����٤��Ǥ���)�Τˤ�������
Ũ¦���ѿ��Ϥ����餫����뤳�ȤϤǤ��ʤ���
����
����ΤĤ��Ƥ���ۤ����Ũ¦�פ��ѿ��ȸ��뤳�Ȥˤ��褦��
̣��¦���ѿ��Ϥ�����Ƿ������ɤ�(����٤��Ǥ���)�Τˤ�������
Ũ¦���ѿ��Ϥ����餫����뤳�ȤϤǤ��ʤ���
����
![]() ���ǽ�Ū����Ω���뤳�Ȥ��̣���ξ�����
�ȸƤ٤С�
��ξ�����̣����ɬ���Ǥ���(�褦��̣������ά������)���Ȥ�ɽ���Ƥ��롣
���ǽ�Ū����Ω���뤳�Ȥ��̣���ξ�����
�ȸƤ٤С�
��ξ�����̣����ɬ���Ǥ���(�褦��̣������ά������)���Ȥ�ɽ���Ƥ��롣
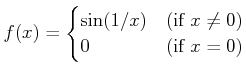
![]() ��
�� ![]() �ˤ�����Ϣ³���᤹�Τϡ��ʲ��Τ褦�ʥ�������ά��ͤ��Ƥ���Τ�Ʊ���Ǥ��롣
�ˤ�����Ϣ³���᤹�Τϡ��ʲ��Τ褦�ʥ�������ά��ͤ��Ƥ���Τ�Ʊ���Ǥ��롣