


Next: About this document ...
��ʬ��ʬ�س���AI���� No.10

��� 10.1
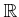
����ʬ����
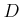
���������줿
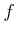
��
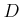
��Ϣ³�Ǥ���Ȥϡ��������������Ƥ���
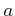
��Ϣ³�Ǥ��뤳�ȡ����ʤ����
������Ω�ĤȤ��˸�����
�������ϡ�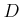 ������֤��Ķ�֤˸¤餺������Ū��
Ŭ�ѤǤ�����ǽҤ٤��Ƥ��롣�ܤ�����¿�ѿ��ξ��˾�������
������֤��Ķ�֤˸¤餺������Ū��
Ŭ�ѤǤ�����ǽҤ٤��Ƥ��롣�ܤ�����¿�ѿ��ξ��˾�������
���֤��Թ�ǽҤ٤�ΤϾ�ά���뤬���˸¤ˤĤ��Ƥ�Ʊ�ͤΤ��Ȥ��餬
����Ω�ġ����ʽ�����1.10�ȤΤ��ȡ�
��������ϡ�����������¿�ѿ��Ǥ��Ѥ���Ȥ�ä����䤫�˾��������
���� 10.4
��Ĥ�Ϣ³�ؿ��ι����ؿ���Ϣ³�Ǥ��롣
���� 10.5 (``���ʽ�����1.13'')
�ؿ�
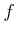
��
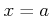
��Ϣ³�Ȥ���
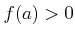
�Ȥ��롣���ΤȤ���
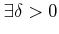
�ǡ�
����������Τ�¸�ߤ��롣
���Τ��Ȥϡ���Ϣ³ 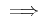 ����դ��Ĥʤ��äƤ���פȤ������Ȥ�
ɽ��ˡ�ΰ�Ĥȸ����롣
����դ��Ĥʤ��äƤ���פȤ������Ȥ�
ɽ��ˡ�ΰ�Ĥȸ����롣
���� 10.6 (``���ʽ�����1.14'', ����ͤ�����)
�ؿ�
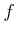
���Ķ��
![$ [a,b]$](img21.png)
��Ϣ³(���ʤ����
![$ [a,b]$](img21.png)
�γ�����Ϣ³)�Ȥ��롣
���ΤȤ�
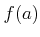
��
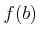
����֤���
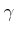
�ˤ������ơ�
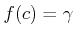
��ߤ����褦��
![$ c\in [a,b]$](img26.png)
��¸�ߤ��롣
��������ϡ�����������ˤ����ơ�Ϣ�뽸���Ϣ³����Ϣ��Ǥ���פȤ���
�����˰��̲�����롣
(��֤ϼ¿�ľ����Ϣ����ʬ����Ȥ�����ħ�Ť��뤳�Ȥ��Ǥ��롣)
���� 10.1
�Ȥ����ȡ�
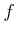
��
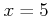
�ˤ�����Ϣ³�Ǥ��뤳�Ȥ�����9.2��(��)�ˤ������ä�
(�Ĥޤꡢ���������ã���Ѥ�����)
�������ʤ�����
���� 10.2
�Ȥ����ȡ�
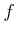
��
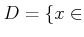
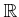
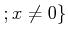
�ˤ�����Ϣ³�Ǥ��뤳�Ȥ�
����ˤ������ä�
�������ʤ�����
����8.1 ������
�Ǥ��롣���������
Ǥ�դ�
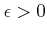 �ˤ������ơ�
�ˤ������ơ�
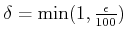 �Ȥ�����
����ȡ�
�Ȥ�����
����ȡ�
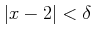 ���������褦�� Ǥ�դ�
���������褦�� Ǥ�դ� 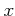 ���Ф��ơ�
���Ф��ơ�
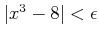 �Ȥʤ뤳�Ȥ��ʲ��˼�������
��ñ�Τ��ᡢ
�Ȥʤ뤳�Ȥ��ʲ��˼�������
��ñ�Τ��ᡢ
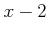 ����ޤ뿷�����ѿ�
����ޤ뿷�����ѿ� 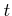 �������ơ�
�������ơ�
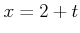 ���ѿ��Ѵ����뤳�Ȥˤ��롣
���ѿ��Ѵ����뤳�Ȥˤ��롣
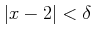 �ˤ�ꡢ
�ˤ�ꡢ
-
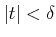
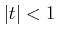
������Ω�Ĥ��Ȥ����դ��롣
| |
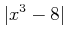 |
|
 |
 |
|
 |
 ���Ÿ�� ���Ÿ�� |
|
 |
 ���������� ���������� |
|
 |
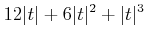 |
|
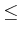 |
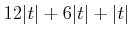 ( ( 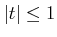 ������)
������) |
|
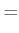 |
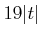 |
|
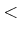 |
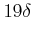
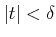 ������)
������) |
|
 |
 |
|
 |
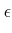 |
|
���ʤꤿ�ġ�
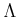
����: �����ʸ����ɽ�����褦�ʿ� (
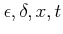 �ʤ�)��
��������
���ܤ��褦��
�ʤ�)��
��������
���ܤ��褦��
�ʾ�ˡ���ξ����Ρ�4�Ĥβ�������ʬ�Ƥߤ롣
- ���ο�
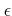 ��Ϳ�����Ƥ��롣���ؤǡ�Ǥ�աפȤ������ˤ�
�ؤɤ���ͤ���Ƥ�ʲ��ε���������פǤ��롣�٤Ȥ�����̣�Ǥ��롣
�������äơ�
��Ϳ�����Ƥ��롣���ؤǡ�Ǥ�աפȤ������ˤ�
�ؤɤ���ͤ���Ƥ�ʲ��ε���������פǤ��롣�٤Ȥ�����̣�Ǥ��롣
�������äơ�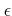 ���ͤ��������ҥȤ��Թ�ˤ�ä��ѹ������ꤹ�뤳�Ȥ�
�Ǥ��ʤ���
���ͤ��������ҥȤ��Թ�ˤ�ä��ѹ������ꤹ�뤳�Ȥ�
�Ǥ��ʤ���
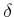 ���ͤ���Ƥ��롣�����ͤϾ����Τʤ��Ǵ��˷�ޤäƤ���ǡ���
(�����
���ͤ���Ƥ��롣�����ͤϾ����Τʤ��Ǵ��˷�ޤäƤ���ǡ���
(���ξ��� 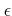 ) ����ޤä���ü�˳μ¤˷�ޤ롣
) ����ޤä���ü�˳μ¤˷�ޤ롣
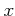 ���о줷��������� ����줿�ϰ�
���о줷��������� ����줿�ϰ�
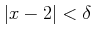 ��ư����롣
����ʳ��ˤ�
�ؤɤ���ͤ���Ƥ�ʲ��ε���������פǤ���٤褦�˰ʲ��ε������Ȥ�Ω�Ƥ�
ɬ�פ����롣
��ư����롣
����ʳ��ˤ�
�ؤɤ���ͤ���Ƥ�ʲ��ε���������פǤ���٤褦�˰ʲ��ε������Ȥ�Ω�Ƥ�
ɬ�פ����롣
 �Ϸ����ؤΤ���Ρ����������Ǥ��롣
�����ͤ�
�Ϸ����ؤΤ���Ρ����������Ǥ��롣
�����ͤ�  ���ͤ���μ¤˷�ޤ롣
���ͤ���μ¤˷�ޤ롣
ARRAY(0x8e5ae10)



Next: About this document ...
2009-06-22
![]()
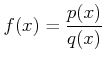 ($p,q$ �� $x$ ��¿�༰)
($p,q$ �� $x$ ��¿�༰)
![]() ����դ��Ĥʤ��äƤ���פȤ������Ȥ�
ɽ��ˡ�ΰ�Ĥȸ����롣
����դ��Ĥʤ��äƤ���פȤ������Ȥ�
ɽ��ˡ�ΰ�Ĥȸ����롣
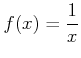
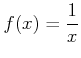
![]() �ˤ������ơ�
�ˤ������ơ�
![]() �Ȥ�����
����ȡ�
�Ȥ�����
����ȡ�
![]() ���������褦�� Ǥ�դ�
���������褦�� Ǥ�դ� ![]() ���Ф��ơ�
���Ф��ơ�
![]() �Ȥʤ뤳�Ȥ��ʲ��˼�������
��ñ�Τ��ᡢ
�Ȥʤ뤳�Ȥ��ʲ��˼�������
��ñ�Τ��ᡢ![]()
![]() ����ޤ뿷�����ѿ�
����ޤ뿷�����ѿ� ![]() �������ơ�
�������ơ�
![]() ���ѿ��Ѵ����뤳�Ȥˤ��롣
���ѿ��Ѵ����뤳�Ȥˤ��롣
![]() �ˤ�ꡢ
�ˤ�ꡢ
![]() �ʤ�)��
��������
���ܤ��褦��
�ʤ�)��
��������
���ܤ��褦��