��ʬ��ʬ�س���AI���� No.8

���󤫤顢�ؿ����ä�����ν����򤦤Ĥ���

���줫�顢 ��$a$ �ζ᤯���������Ƥ���(�¿���)�ؿ� $f$ �� �Ȥ����������������뤳�Ȥ����롣����ϡ� ������Ĥξ�����Ʊ������­���Ƥ��뤳�Ȥ� ����ɽ�����դǤ��롣

1. $f$ �� $\mbox{${\mathbb{R}}$}$ �Τ�����ʬ���� $S$ ���������Ƥ���ؿ� ( $f: S\to$   $\mbox{${\mathbb{R}}$}$ )�Ǥ��롣
2. $S$ �� $a$ ��ޤढ�볫��� $I$ ����ʬ����Ȥ��ƴޤ�

��� 8.1 ( ``1.3.2'' )  

$f$ �ϼ¿� $a$ �ζ᤯��������줿�ؿ��Ǥ���Ȥ��롣���ΤȤ��� $x$ �� $a$ �˶�Ť��Ȥ��� $f(x)$ ���˸��� �� $A$ �Ǥ��� (��$x\to a$ �ΤȤ� $f$ �� $A$ �˼�«����פȤ����) �Ȥϡ�

$$\forall \epsilon>0, \exists \delta>0; ( 0<\vert x-a\vert<\delta \implies \vert f(x)-A\vert<\epsilon)$$

�����������Ȥ��˸�����

($x\to a$ �β����ˤ����ơ���$x=a$ ������ʤ��פȤ����Τ� ��ĤΥݥ���ȤǤ��롣����ϡ�

$$\lim_{x\to a}\frac{\sin(x)-\sin(a)}{x-a}=\cos(a)$$

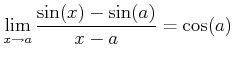
�Τ褦��������ζ˸¤����ˤ��뤳�Ȥ�¿������Ǥ��롣 )

���� 8.2   �������ξ����Τ�Ȥǡ��ؿ� $f(x)$ �� $x$ �� $a$ �˶�Ť��Ȥ��ζ˸��ͤ� ¸�ߤ���Ȥ����ͣ��ĤǤ��롣

��� 8.3   $f(x)$ �� $x\to a$ �ζ˸¤�(���줬�⤷¸�ߤ���С�)

$$\lim_{x\to a} f(x)$$

�Ȥ�����

��� 8.4 ( ``1.3.3'' )  

$f$ �ϼ¿� $a$ �ζ᤯��������줿�ؿ��Ǥ���Ȥ��롣���ΤȤ��� $x$ �� $a$ �˶�Ť��Ȥ��� $f(x)$ �����˸��� �� $A$ �Ǥ��� (�� $x\downarrow a$ �ΤȤ� $f$ �� $A$ �˼�«����פȤ����) �Ȥϡ�

$$\forall \epsilon>0, \exists \delta>0; ( 0<x-a<\delta \implies \vert f(x)-A\vert<\epsilon)$$

�����������Ȥ��˸�����$f$ ����� $a$ ��Ϳ����줿�Ȥ������˸��ͤ� �⤷¸�ߤ���а��Ū�Ǥ��롣�����

$$\lim_{x\downarrow a} f(x)$$    ���뤤�� $$\lim_{x\to a+0} f(x)$$

�Ƚ񤯡����˸�����Ʊ�ͤ��������롣

���� 8.1  

$$\lim_{x\to 2} x^3$$

�Ϥ����餫��(��̤����������Ȥ�˸¤�����˴�Ť��ƾ������衣)

���󡢡֥��������ץ��פ��ꤷ�Ʋ�������ޤ������� ����ϡ����δ֤Υ��󥱡��Ȥη�̤�Ƨ�ޤ�����Τǡ� ����������:

1. �ֵ��κǽ��5ʬ�֤��餤����⥿��������Ƥޤ���
2. �ֵ���ʬ����ʤ��Ȥ������ͤ������ɤ�ʬ����ʤ��Ȥ����ʤɤ� ��ݡ��Ȥ�����Ū���񤤤ơ֤���ˤĤ��Ʋ��⥿����Dz��⤷���ߤ����� �Ȥ���������˾����ĺ����ФǤ���¤ꤪ�������ޤ���
3. ����¾�����Τ褦�ʡ֥ĥܡפ�����˺ܤ���褦�ˤ��ޤ���

�� ���Ĥˤʤä���

$a_n=\frac{1}{n}$ �Ȥ��������ͤ��褦�� ��������С����ӥȥ��󤬰����˰��ٿ������äƤ���Ƥ���ȹͤ�����ɤ���

$$a_1=1$$ 1���� 

$$a_2=0.5$$ 2���� 

$$a_3=0.33333\dots$$ 3���� 

$$a_4=0.25$$ 4���� 

$$a_5=0.2$$ 5���� 

$$a_6=0.1666\dots$$ 6���� 

$$a_7=0.14285714\dots$$ 7���� 

���Ĥˤʤä��� $a_n$ ���ͤ� $0.01$ ��꾮�����ʤ����������

����101���ܡ�

���Ĥˤʤä��� $a_n$ ���ͤ� $0.001$ ��꾮�����ʤ����������

����1001���ܡ�

���Ĥˤʤä��� $a_n$ ���ͤ� $0.000234$ ��꾮�����ʤ����������

(����äȹͤ���)����4274���ܡ�

��������ʹ����Ƥ��Ƥ����ݤ���������Ѥ��Ƽ�ư�����褦��

���Ĥˤʤä��� $a_n$ ���ͤ� $\epsilon(>0)$ ��꾮�����ʤ����������

���� $\lceil 1/\epsilon \rceil$ ( $1/\epsilon$ ����礭���Ǿ�������)���ܡ�

Ʊ�ͤˡ����Ĥˤʤä���

$$\frac{12 n^2 +25 n +2009} { n^2 +6 n +8}$$

�� $12$ �Ȥκ��� $0.1$ �ʲ��ˤʤ��������

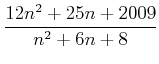
��������Ū�ʷ׻��פ����򤹤뤿���

(a)ɽ�ˤϿ���΢�ˤϥ���ե��٥åȤν񤫤줿�����ɤ�4�礢�롣 ������ A, K, 4, 7 �Ǥ��ä��� �����Υ����ɤΤ��Ȥ��Ȥ��� ���첻��΢¦�ο�����ɬ�������ˤʤäƤ���� �Ȥ����롼�����­���Ƥ��뤳�Ȥ�Τ���뤿��ˤϡ� ����Dz���Υ����ɤ�᤯��ɬ�פ����뤫��(�����ϤɤΥ����ɤ���)

(b)4�ͤΥҥȤ����롣

• �ӡ�������Ǥ���ҥ�(ǯ���Ծܡ�)
• ��������Ǥ���ҥ�(ǯ���Ծܡ�)
• ���������Ǥ���24�Ф���ǯ��
• ���������Ǥ���16�Ф����̡�

�����ΥҥȤΤ��Ȥ��Ȥ��� ��20��̤���ϥ��륳��������Ǥϥ����ʥ��� �Ȥ����롼�����­���Ƥ��뤳�Ȥ�Τ���뤿��ˤϡ� ����Dz��ͤΥҥȤˤĤ��ƿ����ʾ��������ɬ�פ����뤫�� (�����ϤɤΥҥȤ���)

�ܺ٤ϡֶ����ס��첻�פǥͥåȤ򸡺�������ɤ��� �ɤ�������꤬ʬ����䤹������������(������� File-071���)

����ݡ��Ȥβ�������

�� ����6.2 �Ǥϡ�$\{a_n\}$ ��ͭ���Ǥ��뤳�Ȥ��������Τ� �ݥ���ȤǤ��롣 ��$\{a_n\}$ ��ͭ���Ȥ��ơ� �Ȥ� ��$\{a_n\}$ ��ͭ���Ȳ��ꤹ��פDz������Ϥޤ�ΤϤΤä����饪��������

�� $\{a_n\}$ �� $c$ �˼�«����Ȥ������Ȥ�̤�� $\lim_{n\to \infty} a_n$ �Ƚ񤯤ΤǤ��롣 $\{a_n\}$ �� ��$\{a_n\}$ �� $c$ �˼�«����Τǡ� $\lim_{n\to \infty} a_n =c$ �� �ʤɤȽ񤯤Τϡ��������򤷤ʤ��Ȥ������ݤ�Ϳ���롣

�� ��«��ñĴ�Ȥϸ¤�ʤ��� �㤨�� $(-1)^n \frac{1}{n}$ �� 0 �� ��«���뤷�� $5+(-1)^n \frac{1}{n}$ �� $5$ �˼�«���롣

�� �ֿ���ͭ���Ǥ���פȤ� $\{a_n\}$ ���Τ� ������ $[N,N']$ �� ���äݤ�����뤳�Ȥ��̣���Ƥ��롣 ��İ�Ĥθ���ͭ���Ǥ��뤫��Ȥ��äơ����Τ�ͭ���Ǥ���Ȥϸ¤�ʤ���