Next: About this document ...
ïŋ―ïŋ―ĘŽïŋ―ïŋ―ĘŽïŋ―Øģïŋ―ïŋ―ïŋ―AIïŋ―ïŋ―ïŋ―ïŋ― No.5
 ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ― 5.1
ïŋ―Âŋïŋ―
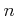
ïŋ―ïŋ― 0
ïŋ―Ęūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
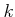
ïŋ―ČĪËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ā·ļïŋ―ïŋ―ïŋ―ČĪïŋ―ÖĄïŋ―
ïŋ―âđŧïŋ―ĮĪïŋ― 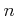 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ÐūėĪ·ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ËĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ÐūėĪ·ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ËĪïŋ―
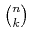 ïŋ―ïŋ―
ïŋ―Ôūïŋ―ïŋ―Îŋïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―Ôūïŋ―ïŋ―Îŋïŋ―ïŋ―ïŋ― 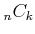 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 5.2 (ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
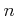
ïŋ―ËĪÄĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĄïŋ―
Ėŋïŋ―ïŋ― 5.3
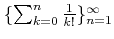
ïŋ―Ïžïŋ―ÂŦïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎķËļÂĪïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―Îĩïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆŧČĪÃĪïŋ―)
ïŋ―Č―ņĪŊĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 5.4 (``ïŋ―ïŋ―1.8'')
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―
-
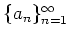 ïŋ―ïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ÃĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ÃĪĮĪïŋ―ïŋ―ëĄĢ
- ĮĪïŋ―ÕĪïŋ―
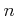 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
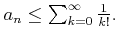
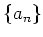 ïŋ―ÏĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍĪËžïŋ―ÂŦïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ÏĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍĪËžïŋ―ÂŦïŋ―ïŋ―ïŋ―ëĄĢ
Proof.
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮšĮļïŋ―ïŋ―ïŋ―ÂĪËļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
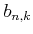
ïŋ―Č―ņĪŊĪČĄïŋ―
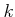
ïŋ―ïŋ―ïŋ―ïŋ―ęĪđïŋ―ëĪīïŋ―ČĪËĄïŋ―
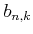
ïŋ―ïŋ―ÃąÄīïŋ―ïŋ―ïŋ―ÃĪĮĄïŋ―
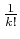
ïŋ―ïŋ―ïŋ―Ïūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
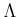
ïŋ―ïŋ―ïŋ― 5.5
ïŋ―ïŋ―ÂŦïŋ―ïŋ―
ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―
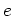
ïŋ―Č―ņĪĄïŋ―ïŋ―ÍĨïŋ―ïŋ―ÔĨïŋ―ïŋ―Îŋïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ðŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČļÆĪÖĄïŋ―
Ėŋïŋ―ïŋ― 5.6
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―
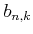
ïŋ―ïŋ―ïŋ―áĪŋïŋ―ČĪïŋ―ïŋ―ïŋ―
- ĮĪïŋ―ÕĪïŋ―
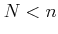 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
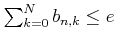 .
.
- ïŋ―ÂĪïŋ―
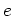 ïŋ―ïŋ―Ėŋïŋ―ïŋ― 5.3 ïŋ―Îŋïŋ―ïŋ―Č°ïŋ―ïŋ―ŨĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―Ėŋïŋ―ïŋ― 5.3 ïŋ―Îŋïŋ―ïŋ―Č°ïŋ―ïŋ―ŨĪïŋ―ïŋ―ëĄĢ
Ėŋïŋ―ïŋ― 5.3 ïŋ―ïŋ―ïŋ―ÂĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―áĪŊïŋ―ïŋ―ÂŦïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 5.1
Äđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―įĪĶïŋ―ÉĄïŋ―
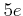
ïŋ―âĪ·ïŋ―ïŋ―ïŋ―ïŋ―
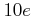
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ᥞïŋ―ČĨïŋ―ïŋ―ïŋ―ÓĪïŋ―ïŋ―ÉŪïŋ―ïŋ―ïŋ―ęĩŽïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ŅĪïŋ―ïŋ―Æšïŋ―ÞĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÓĪËĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ÂĪÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÂĪÎĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ŲĪÞĪĮĪōĩĪĪËĪïŋ―ïŋ―ïŋ―ÉŽïŋ―ŨĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―?
(ïŋ―ÚĪïŋ―ïŋ―ïŋ―ĮĪïŋ―ëĪģïŋ―ïŋ―)
ïŋ―Öĩïŋ―ïŋ―ČĨïŋ―ÝĄïŋ―ïŋ―Čšïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―éĩĪïŋ―ÅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―:
ïŋ―ïŋ―Î―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪÏļïŋ―ïŋ―ïŋ―ōū·Īïŋ―ïŋ―ÞĪïŋ―ïŋ―ÍĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ÂĪïŋ―ïŋ―ïŋ―ïŋ―ėĪūïŋ―ïŋ―ÉĪÎģïŋ―ïŋ―Įīïŋ―Íŋïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŦ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍŧŌĪïŋ―ïŋ―ÓĨïŋ―ïŋ―ïŋ―ÕĪĮ―ņĪąĄïŋ―ÃĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―Äđïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ęĩŽïŋ―ĮĪÏĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ï°ÏĪïŋ―
ïŋ―ïŋ―ïŋ―ÎĪïŋ―) 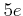 ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïŋ― 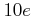 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ᥞïŋ―ČĨïŋ―ËĪïŋ―ïŋ―čĄĢïŋ―ŨĪČĪïŋ―ïŋ―ïŋ―ïŋ―ÛĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪïŋ―
ïŋ―ÞĪïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ßĨÞĨïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ᥞïŋ―ČĨïŋ―ËĪïŋ―ïŋ―čĄĢïŋ―ŨĪČĪïŋ―ïŋ―ïŋ―ïŋ―ÛĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪïŋ―
ïŋ―ÞĪïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ßĨÞĨïŋ―ïŋ―ïŋ―



Next: About this document ...
2009-05-26
![]() ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
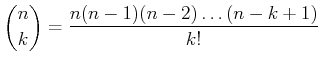
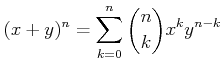
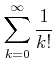
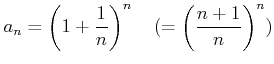
![]()