![]()
![]() ����Ȥϡ� ���դλȤ����ΤȤ꤭��Τ��ȤǤ�����
���ؤǤϡ��ɤΤ褦�ʸ��դ⡢���Τ褦�ʼ����ʤ��ǻȤ��뤳�ȤϤʤ���
(���������������ס�ͭ�����ס����¡ס����ѡפʤɤθ��դ�����������Τ�
��֤������롣
�����ˤĤ��ƾܺ٤��������Τ�
���ιֵ��ǤϹ����롣
(üŪ�˸����С������ϵ�Ǽˡ����Ѥ����������
ͭ�����������Ρ־���
����Ȥϡ� ���դλȤ����ΤȤ꤭��Τ��ȤǤ�����
���ؤǤϡ��ɤΤ褦�ʸ��դ⡢���Τ褦�ʼ����ʤ��ǻȤ��뤳�ȤϤʤ���
(���������������ס�ͭ�����ס����¡ס����ѡפʤɤθ��դ�����������Τ�
��֤������롣
�����ˤĤ��ƾܺ٤��������Τ�
���ιֵ��ǤϹ����롣
(üŪ�˸����С������ϵ�Ǽˡ����Ѥ����������
ͭ�����������Ρ־��� ![]() ��Ŭ���ʡ����������ɤ�����Ƚ�구§�פ�
������롣)
�����ˤĤ��ƾܺ٤��������Τ�
���ιֵ��ǤϹ����롣
�¿���ͭ�����ζ˸¤Ȥ���
�������Τ����������Ϥ��Ρֶ˸¡פ�����Ǥ��롣)
��Ŭ���ʡ����������ɤ�����Ƚ�구§�פ�
������롣)
�����ˤĤ��ƾܺ٤��������Τ�
���ιֵ��ǤϹ����롣
�¿���ͭ�����ζ˸¤Ȥ���
�������Τ����������Ϥ��Ρֶ˸¡פ�����Ǥ��롣)
![]()
![]() ��
�� ![]() �ȤϤʤˤ���
�ȤϤʤˤ���
�ϡ��֤ɤ��
�ϡ��֤ʤˤ������Ĥ�
�������������ΤΤ��Ȥιֵ��Ǥ�
![]() �Ƚ�
����Ȥϡ�����Ū�ˤϼ��Τ褦������Ǥ��롣
�Ƚ�
����Ȥϡ�����Ū�ˤϼ��Τ褦������Ǥ��롣
���ּ�«����פȤ������Ȥθ�̩������褦�� ����ˤϡ������ͤ��Ѥ��롣
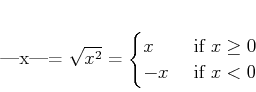
(������ʿ������0�ʾ�Τۤ������֡�)
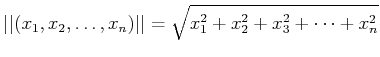
���λ�����������¤Ϲ⼡���ξ��ˤ�����Ω�ġ�
���ʤꤿ�ġ�
���褤���«���������Ҥ٤褦��
���ʤꤿ�ĤȤ��˸�����
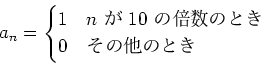
���������Ȥ���
(����) ����ˡ�ǡ�![]() �������
������� ![]() �˼�«�����Ȥ��롣
��«�������
�˼�«�����Ȥ��롣
��«������� ![]() �Ȥ���
�Ȥ���
![]() ����Ѥ��褦��
����
����Ѥ��褦��
���� ![]() ��¸�ߤ��ơ�
��¸�ߤ��ơ�
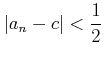 |
(��) |
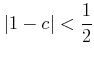
���狼�ꡢ
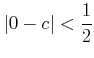
���狼�롣
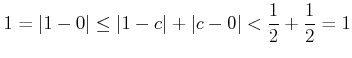
�Ȥʤä�̷��Ǥ��롣
��äơ�![]() �Ϥ����ʤ��ͤˤ��«���ʤ���
�Ϥ����ʤ��ͤˤ��«���ʤ���
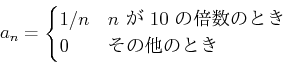
���������Ȥ���
(����)
Ϳ����줿
![]()
![]()
![]() �ˤ������ơ�
�ˤ������ơ�
![]() �Ȥ��ơ�
�Ȥ��ơ�
![]() ����礭���������ĤȤäƤ�����
(���Τ褦�ʤ��(���ʤ��Ϳ����줿�¿������礭������)
��¸�ߤ��뤳�Ȥϡ��֥��륭��ǥ��θ����פȤ���
�ݾڤ���Ƥ��뤬���ޥ����������äƤ����������ȻפäƤ��ɤ���)
����礭���������ĤȤäƤ�����
(���Τ褦�ʤ��(���ʤ��Ϳ����줿�¿������礭������)
��¸�ߤ��뤳�Ȥϡ��֥��륭��ǥ��θ����פȤ���
�ݾڤ���Ƥ��뤬���ޥ����������äƤ����������ȻפäƤ��ɤ���)
���� ![]() ����«�������
����«������� ![]() ������̤������Ȥ�����
�ºݡ�
������̤������Ȥ�����
�ºݡ� ![]() �ʤ�Ǥ�դ�
�ʤ�Ǥ�դ� ![]() �ˤ������ơ�
�ˤ������ơ�
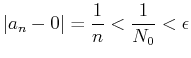
�Ȥʤäơ�������ξ��ˤ���
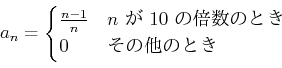
���������Ȥ���