Next: About this document ...
ïŋ―ïŋ―ïŋ―Ïģïŋ― IAïŋ―é―Ž No.9
 ïŋ―ïŋ―Îķïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―Âŋïŋ―ïŋ―ÍĪâĪ·ïŋ―ïŋ―ïŋ―ÏĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―)
ïŋ―Øŋïŋ―
ïŋ―ïŋ―Îķïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―Âŋïŋ―ïŋ―ÍĪâĪ·ïŋ―ïŋ―ïŋ―ÏĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―)
ïŋ―Øŋïŋ― 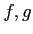 ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―éĨ°ïŋ―ïŋ―óĨļĨïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ÏĄïŋ―
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―éĨ°ïŋ―ïŋ―óĨļĨïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ÏĄïŋ―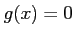 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ― 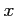 ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
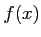 ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ÍĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪËŧČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ÍĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪËŧČĪïŋ―ïŋ―ëĄĢ
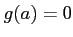 ïŋ―ĘĪïŋ―
ïŋ―ĘĪïŋ― 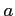 ïŋ―ïŋ―
ïŋ―ïŋ― 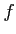 ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―čĪĶïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―čĪĶïŋ―ïŋ―
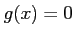 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 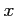 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ĖĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―ïŋ―ïŋ―ÎĄïŋ―)ïŋ―Įķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―Îķïŋ―ïŋ―Öūïŋ― 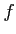 ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪÏĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪÏĄïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ęĪģïŋ―ïŋ―ïŋ―
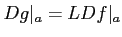 ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 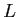 ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―Æąïŋ―ÍĪĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―Æąïŋ―ÍĪĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ― 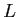 ïŋ―ïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŨĪČĪïŋ―ïŋ―ÆĪïŋ―ïŋ―éĪŋïŋ―ïŋ―
ïŋ―Ņŋïŋ―ïŋ―ïŋ―ïŋ―ČĪßđïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ξïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ(ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―ņĪŊĪĘĄïŋ―)
ĖĪïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―Κïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ÏĪïŋ―ïŋ―ÎŧČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢïŋ―Ęēïŋ―ïŋ―Îŋïŋ―ïŋ―ïŋ―ōŧēūČĄïŋ―
ïŋ―ïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŨĪČĪïŋ―ïŋ―ÆĪïŋ―ïŋ―éĪŋïŋ―ïŋ―
ïŋ―Ņŋïŋ―ïŋ―ïŋ―ïŋ―ČĪßđïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ξïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ(ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―ņĪŊĪĘĄïŋ―)
ĖĪïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―Κïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ÏĪïŋ―ïŋ―ÎŧČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢïŋ―Ęēïŋ―ïŋ―Îŋïŋ―ïŋ―ïŋ―ōŧēūČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 9.3 (ïŋ―ïŋ―)
ïŋ―óžĄķïŋ―ïŋ―ïŋ―
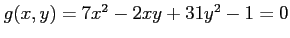
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪČĪïŋ―áĪĪïŋ―ïŋ―ïŋ―ČĪïŋ―ÃĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōĪ―ĪėĪūïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ŌĨïŋ―ïŋ―: 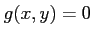 ïŋ―ĘĪïŋ―ïŋ―ïēžïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïēžïŋ―ïŋ― 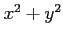 ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―
ĖĪïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―Įĩïŋ―ïŋ―čĄĢ)
ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―
ĖĪïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―Įĩïŋ―ïŋ―čĄĢ)
ïŋ―ïŋ―ïŋ―ïŋ― 9.4
ïŋ―ïŋ―ïŋ―óžĄķïŋ―ïŋ―ïŋ―
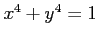
ïŋ―ËĪÄĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ō·ŦĪïŋ―ïŋ―ÖĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 9.5
ïŋ―ïŋ―ïŋ―óžĄķïŋ―ïŋ―ïŋ―
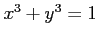
ïŋ―ËĪÄĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ō·ŦĪïŋ―ïŋ―ÖĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ÎĨïŋ―Įūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―...)
ïŋ―ïŋ―ïŋ―ïŋ― 9.6
ïŋ―ïŋ―ïŋ―
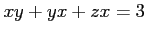
,
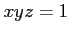
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
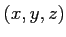
ïŋ―ÎĪĘĪïŋ―ïŋ―ĮĄïŋ―
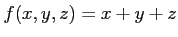
ïŋ―ïŋ―ïŋ―ÍĪïŋ―
ïŋ―ïŋ―Îąïŋ―ÍĪōļŦĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ÍĪïŋ―ïŋ―ÆĄïŋ―
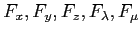
ïŋ―Îķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪáĄĒ
Âģïŋ―ïŋ―ïŋ―ïŋ―
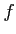
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïēžïŋ―ĮĪïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ÍĪïŋ―ïŋ―ČĪïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 9.8 (ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―1)
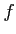
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―ïŋ―
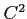
ïŋ―ïŋ―Øŋïŋ―ïŋ―Čēïŋ―ïŋ―ęĪđïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
- ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽÉūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
-
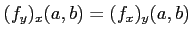 ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 9.9
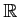
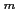
ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
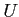
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ėĪŋ
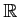
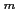
-ïŋ―ïŋ―
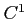
ïŋ―Øŋïŋ―
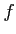
ïŋ―ïŋ―
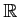
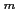
ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
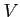
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ėĪŋ
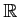
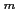
-ïŋ―ïŋ―ÏĒÂģïŋ―Øŋïŋ―
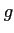
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ÆĄïŋ―
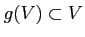
ïŋ―ïŋ―ïŋ―ïŋ―
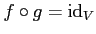
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÃĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―âĪ·ïŋ―ïŋ―ïŋ―ïŋ―
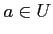
ïŋ―ïŋ―
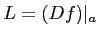
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆēÄĩïŋ―(ïŋ―ÄĪÞĪęĄĒ
ïŋ―Õđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
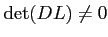
)ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ČĄïŋ―
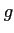
ïŋ―ïŋ―
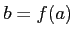
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―Į―ïŋ―ĮĪïŋ―ïŋ―ÃĪÆĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĪïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ŌĨïŋ―ïŋ―:
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĪïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―
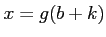 ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―
ïŋ―ïŋ―ïŋ―ČĪïŋ― 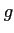 ïŋ―ïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÜĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ÏĒÂģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÜĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―)



Next: About this document ...
2009-07-29
 .
.
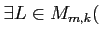
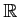
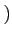 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ― 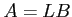 ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĄïŋ―
![]()
![]() ïŋ―ïŋ―Îķïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―Âŋïŋ―ïŋ―ÍĪâĪ·ïŋ―ïŋ―ïŋ―ÏĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―)
ïŋ―Øŋïŋ―
ïŋ―ïŋ―Îķïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―Âŋïŋ―ïŋ―ÍĪâĪ·ïŋ―ïŋ―ïŋ―ÏĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―)
ïŋ―Øŋïŋ― ![]() ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―éĨ°ïŋ―ïŋ―óĨļĨïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ÏĄïŋ―
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―éĨ°ïŋ―ïŋ―óĨļĨïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ÏĄïŋ―![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ― ![]() ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ÍĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪËŧČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ÍĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪËŧČĪïŋ―ïŋ―ëĄĢ
![]() ïŋ―ĘĪïŋ―
ïŋ―ĘĪïŋ― ![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―čĪĶïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―čĪĶïŋ―ïŋ―
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―