Next: About this document ...
ïŋ―ïŋ―ïŋ―Ïģïŋ― IAïŋ―é―Ž No.8
ïŋ―ïŋ―ïŋ―ïŋ― 8.3
ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Øŋïŋ―
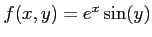
ïŋ―ÎĨïŋ―ïŋ―ïŋ―ïŋ―
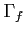
ïŋ―ËĪÄĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―
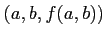
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
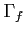
ïŋ―ïŋ―ïŋ―ïŋ―Ęŋïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 8.4
ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Øŋïŋ―
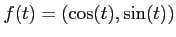
ïŋ―ÎĨïŋ―ïŋ―ïŋ―ïŋ―
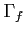
ïŋ―ËĪÄĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―
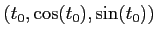
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
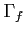
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 8.6
ïŋ―ÐģŅđïŋ―ïŋ―ïŋ―
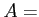
diag
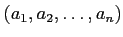
ïŋ―ËĪÄĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―Îđïŋ―ïŋ―ïŋ―ÎĨïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―



Next: About this document ...
2009-06-16
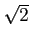 ïŋ―Îķïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Îķïŋ―ïŋ―ïŋ―ïŋ― 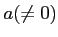 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
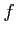 ïŋ―ïŋ―
ïŋ―ïŋ― 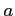 ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 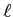 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―áĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―áĄĒ 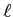 ïŋ―ïŋ―
ïŋ―ïŋ― 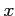 ïŋ―ïŋ―ïŋ―ČĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ČĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 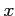 ïŋ―ïŋ―Éļïŋ―ïŋ―
ïŋ―ïŋ―Éļïŋ―ïŋ― 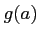 ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―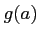 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ― 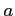 ïŋ―Ξïŋ―ïŋ―Į―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ξïŋ―ïŋ―Į―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
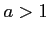 ïŋ―ĘĪïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ― 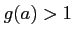 ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
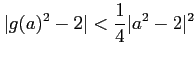
![$ a\in [1,4]$](img13.png) ïŋ―ĘĪïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―
![$ g(a) \in [1,4]$](img14.png) ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
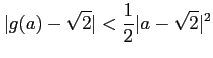
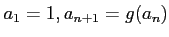 ïŋ―ΚĮ―ïŋ―Îŋïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―Åļïŋ―ïŋ―(ïŋ―ïŋ―ĖĢïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪĮĪïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
((1)-(3) ïŋ―ïŋ―ïŋ―ōĪąĪïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪČĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―)
ïŋ―ΚĮ―ïŋ―Îŋïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―Åļïŋ―ïŋ―(ïŋ―ïŋ―ĖĢïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪĮĪïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
((1)-(3) ïŋ―ïŋ―ïŋ―ōĪąĪïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪČĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―)